Question
Question: “During refraction of light through the glass slab, incident ray and emergent ray are parallel to ea...
“During refraction of light through the glass slab, incident ray and emergent ray are parallel to each other.” Explain.
Solution
Hint: This problem can be solved by using Snell’s law at both edges (the edge at which the incident ray enters the slab and the edge at which the emergent ray leaves the slab) of a glass slab. Therefore, we can find out a relation between the respective angles of incidence and angles of refraction at both edges which will help us to explain the question statement.
Formula used:
When light travels from a medium of optical density n1 into another medium of optical density n2, the angle of incidence i and angle of refraction r at the interface is related by
n1sini=n2sinr (Snell’s Law)
Complete step by step answer:
Let us start off by drawing a diagram.
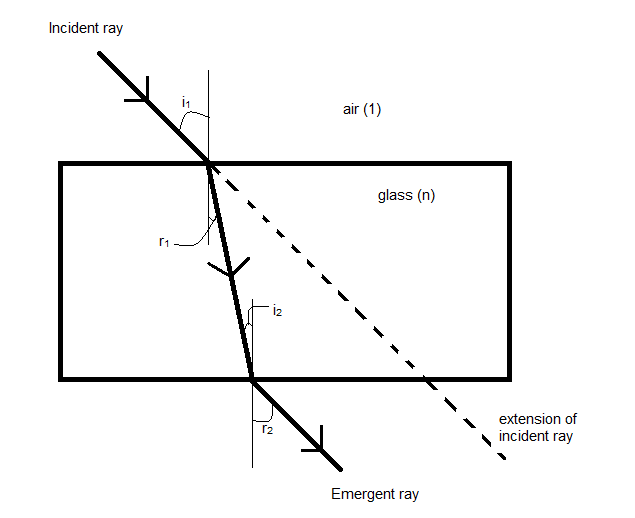
Here, we have a light ray entering into a glass slab of refractive index n at an angle of incidence i1 from air (refractive index of 1).
The emergent ray leaves the glass slab from the other edge with the angle of refraction r2 as shown.
The incident ray has been extended virtually to show its path in the absence of the glass slab.
When light travels from a medium of optical density n1 into another medium of optical density n2, the angle of incidence iand angle of refraction rat the interface is related by
n1sini=n2sinr (Snell’s Law) --(1)
The angle of refraction at the incident edge is r1 and the angle of incidence at the emergent edge is i2.
Now, applying (1) at the incident edge, we get,
1×sini1=n×sinr1
∴sini1=nsinr1 --(2)
Now, the light ray in the glass slab acts as a transversal between two parallel vertical lines.
Hence,
r1=i2 (They are alternate interior angles) --(3)
Now, applying (1), at the emergent edge, we get,
n×sini2=1×sinr2
∴nsini2=sinr2
∴nsinr1=sinr2 (Using (3))
∴sini1=sinr2 [Using (2)]
∴i1=r2
Hence, the incident ray and the emergent ray make the same angle with the vertical. Hence, since lines which make the same angle with another line are parallel, therefore, the incident ray and emergent ray are parallel.
Therefore, during refraction of light through the glass slab, incident ray and emergent ray are parallel to each other.
Note: In optics, the main approach to solving a problem should be to draw a proper diagram. By drawing a proper diagram, relations can be found out between different variables in the problem by using geometry, construction or trigonometry. The diagram also makes the question very easy to visualize, since our brain is better able to remember and understand a picture.
Though the incident and emergent ray are parallel to each other, the emergent ray has been laterally shifted. This happens while light goes through a glass slab. This is known as the lateral displacement. This is the reason why the letters of a newspaper seem to get shifted when a glass slab is kept over it.
