Question

During an experiment a signal from a spaceship reached the ground station in five minutes. What was the distance (in m) of the spaceship from the ground station? The signal travels at the speed of light that is,
$3 \times {10^8}m/s$.

Answer 1

Rate of change of velocity is acceleration and rate of change of displacement is velocity. We have kinematic formulas which will relate the velocity and displacement and the acceleration. Here in the given question spaceship doesn’t have any acceleration but has only constant velocity.
Formula used:
$s = vt$

Complete answer:
DISTANCE-
It is the total length travelled by a particle in a certain time interval. The path in which it travels matters too. It is a scalar quantity i.e it has only magnitude. Since it has only magnitude it is Always positive. Its value will be greater than or equal to the displacement. Its unit is meter
DISPLACEMENT-
It is the shortest distance or shortest length the particle had travelled in a given time interval. Path of travel doesn’t matter over here. It is a vector quantity so it has both direction and magnitude. It can be positive or negative or even can be zero. It can never be greater than distance it is always lesser than or equal to distance. Its unit is meter.

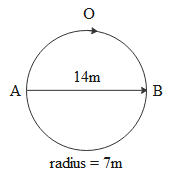
In the above circle if a particle had travelled from A to B along AOB then distance is half of the perimeter of the circle i.e 22m while displacement is its diameter i.e 14m and if it reaches point A again then distance is its perimeter 44m while displacement is zero.
Now coming to the question asked, let us assume that the spaceship signal had travelled in a straight line, that means distance will be equal to displacement. Direction of velocity will always be along the direction of motion.
So we can apply the formula
$s = vt$
Velocity is given as $3 \times {10^8}m/s$ and time is given as 5 minutes that means $5\min = 5 \times 60\sec = 300\sec$
So by substituting the values we get distance as
$s = vt$
\eqalign{ & \Rightarrow s = \left( {3 \times {{10}^8}m/s} \right)\left( {300s} \right) \cr & \therefore s = 9 \times {10^{10}}m \cr}
Hence the distance will be $9 \times {10^{10}}m$

Note:
The main reason why we had differentiated between distance and displacement is we were asked to find out the distance between the spaceship and the ground. We can apply the above kinematic equation only to find out the displacement. The only option we have is distance and displacement are the same here and finding the asked value.