Question
Question: Due to friction, the system as shown in the diagram remains motionless. Calculate the static coeffic...
Due to friction, the system as shown in the diagram remains motionless. Calculate the static coefficient of friction?
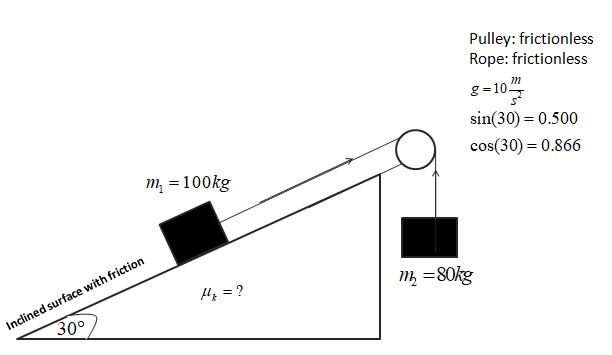
Solution
First, the weights of the given masses have to be divided into two components: horizontal and vertical. Thereafter, the forces acting on the masses have to be concluded. The formula of the frictional force has to be known in terms of the static coefficient of friction. The value of the static coefficient of friction can be found in the equation of forces.
Formula used:
The static frictional force, fs=T−m1gsinθ
Tis the tension of the string.
m1gsinθ is the sine component of the weight of mass m1
fs=μN μis the static coefficient of friction.
The normal force, N=m1gcosθ
T=m2g
Complete step-by-step solution:
The diagram in the problem is given by,
First, the diagram has to be modified by showing the components of the forces acting on the two masses m1and m2 .
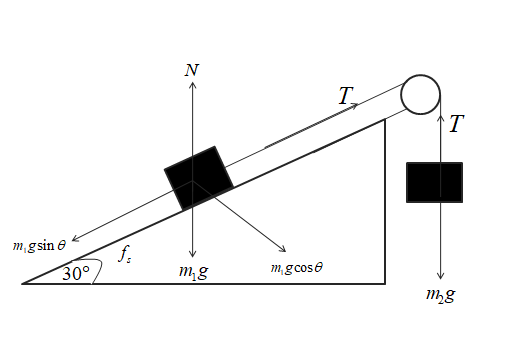
The weight of the mass m1is m1g . It is divided into two components horizontal and vertical at an angle θ(=30∘) i.e. m1gcosθ and m1gsinθ.
The tension of the string is T.
Now, The static frictional force, fs=T−m1gsinθ
From the diagram, it is shown that T=m2g
⇒fs=m2g−m1gsinθ
Now, the formula of the static frictional force in terms of the static coefficient of friction μ,
fs=μN
The normal force, N=m1gcosθ
Now put the values of fs and N, we get
⇒μN=m2g−m1gsinθ
⇒μm1gcosθ=m2g−m1gsinθ
⇒μm1cosθ=m2−m1sinθ
⇒μ=m1cosθm2−m1sinθ
Given that, m1=100kg
m2=80kg
sinθ=sin30=0.500
cosθ=cos30=0.866
⇒μ=(100×0.866)80−(100×0.500)
⇒μ=86.680−50
⇒μ=86.630
⇒μ=0.346
Hence the static coefficient of friction ⇒μ=0.346.
Note: The frictional force is the constraint to the motion of a body having motion relative to another. like gravitational force or electromagnetism, It is not a fundamental force. It is the force between two surfaces that are sliding, or going to slide, across each other. The direction of the frictional force is opposite to the direction of the surface.
There are two types of friction: 1. Static Friction is the highest force by a surface on a body until it remains stationary.
2. Sliding friction is the minimum force needed to keep the body having motion over a surface such that it moves similar distances in equal time.
