Question
Question: Drum B undergoes \(\left( a \right)\) Translational motion. \(\left( b \right)\) Rotational moti...
Drum B undergoes
(a) Translational motion.
(b) Rotational motion.
(c) Rotational as well as translational motion.
(d) None of the above
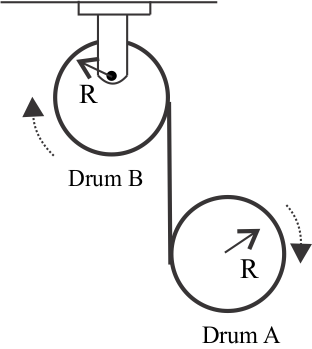
Solution
To answer this type of question, we must know first the translational and rotational motion. Also the torque. With the help of these three terms, we can answer this question. So let’s know first what these three terms mean.
Complete step by step solution:
Translational Motion: translational motion is a motion that involves the slippery of an object in one or additional of the 3 dimensions: x,y or z. However an object will still be moving even once it's simply sitting at a selected x,y or z-coordinate, it will still spin.
Rotational Motion: This motion is defined as wherever an object spins around an enclosed axis in a very continuous approach. A skater will do that by spinning on the spot. She’s going to offer herself rotational energy. And since energy is often preserved and a smaller object should spin quicker to possess constant energy, once she moves her arms in towards her body, her rotation speed can increase - the spinning can get quicker and quicker.
A rigid body performs a true movement motion if every particle of the body moves in a very circle, and also the center of all circles lies on the line (axis of rotation).
Now we will be able to answer this
Since the center of the drum B is fixed. Therefore it will not perform the translational motion.
On the other hand, the rope exerts a torque on the drum B which makes the drum rotate. Therefore we can say that the drum B undergoes the rotational motion.
Hence, it is a rotational motion.
Note: Torque is the measure of the force that may cause an object to rotate concerning an axis. Force is what causes an object to accelerate in linear mechanics. Similarly, torque is what causes an angular acceleration. Hence, torque may be outlined because of the movement equivalent of linear force.
