Question
Question: DRG of $\tan^{-1}\tan x^2$ when $x \in [-1,2]$...
DRG of tan−1tanx2 when x∈[−1,2]
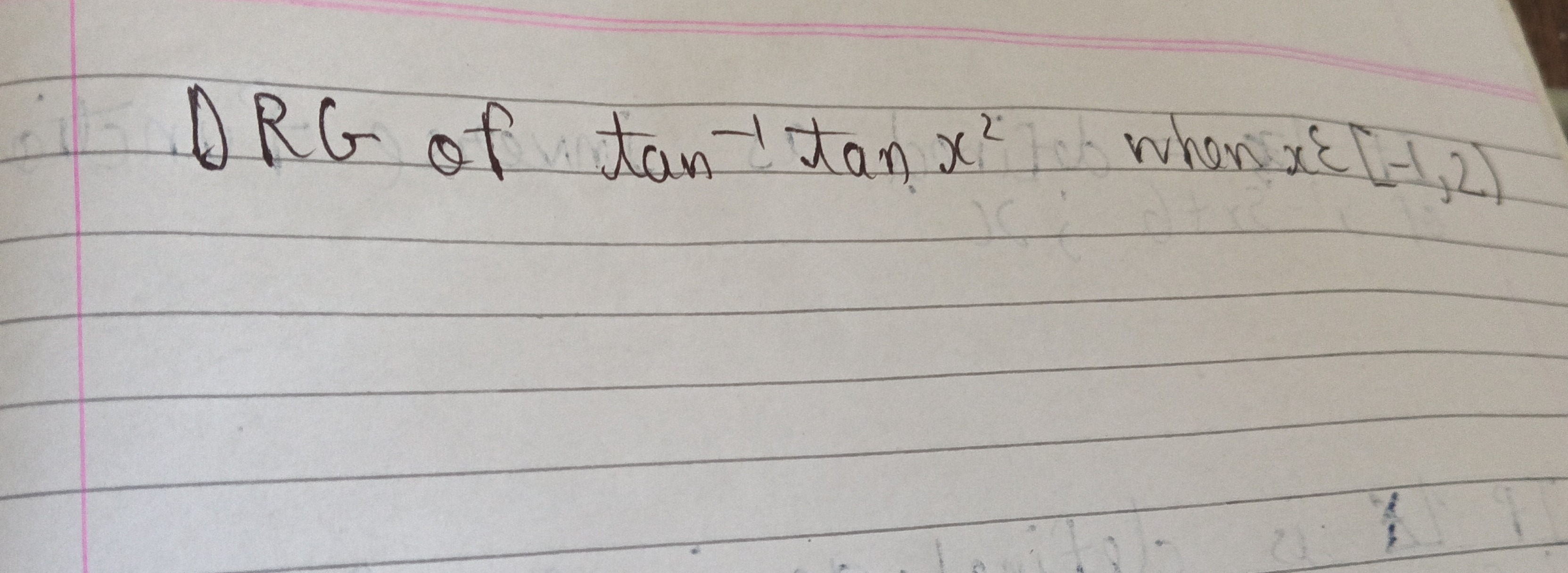
-
Domain: {x∈[−1,2]∣x=π/2}
-
Range: (−2π,2π)
-
Graph:
- For ∣x∣<π/2: y=x2.
- For x∈(π/2,2]: y=x2−π,
with a discontinuity (hole) at x=π/2.
Solution
We wish to simplify
y=tan−1(tan(x2))for x∈[−1,2]. Recall that tan−1 (or arctan) returns the unique value in its principal range (−2π,2π). Thus, for any real number θ,
tan−1(tanθ)=θ−kπ,where k is an integer chosen so that
θ−kπ∈(−2π,2π).Since
θ=x2,and noting that for x∈[−1,2]
x2∈[0,4],we separate the analysis into cases.
1. When is x2 in the principal interval?
We need
x2∈(−2π,2π).Since x2≥0, this becomes
x2∈[0,2π).In this case, no adjustment is needed and
y=x2.2. When is x2 outside the interval (−2π,2π)?
For x2∈[2π,4], we choose k=1 (since x2<3π/2 for x2≤4) so that
x2−π∈(−2π,2π).Thus, for these x,
y=x2−π.3. Domain issues from the definition of tan
Remember that the function tan(x2) is not defined when
cos(x2)=0⟹x2=2π+nπ(n∈Z).Within x2∈[0,4] the only problematic value is:
x2=2π⟹x=±2π.Since x∈[−1,2] and 2π≈1.253, note that
−2π≈−1.253∈/[−1,2].Thus the only point to be removed is
x=2π.Final Answers
Domain:
{x∈[−1,2]:x=π/2}.Range:
Looking at the two pieces:
- For x2∈[0,2π): y=x2 covers [0,2π).
- For x2∈(2π,4]: y=x2−π covers values from just above 2π−π=−2π up to 4−π.
The union of these intervals is
(−2π,2π).Graph:
The function is given piecewise by
- For x such that x2<2π (i.e. ∣x∣<2π), y=x2.
- For x such that x2>2π (i.e. for x∈(2π,2], and symmetrically for x∈[−1,−2π) if such existed in the interval—but note −2π∈/[−1,2]), y=x2−π.
There is a jump discontinuity at x=2π where the function is not defined.
A rough schematic using mermaid:
Minimal Core Explanation
- For x2∈[0,π/2), tan−1(tan(x2))=x2.
- For x2∈(π/2,4], choose k=1 so that tan−1(tan(x2))=x2−π.
- Exclude x such that x2=π/2 (i.e. x=π/2) because tan is undefined there.
- The combined range from the two cases is (−2π,2π).
