Question

Draw the structure of$I{{F}_{7}}$ . Write its geometry and the type of hybridization.

Answer 1

It is a type of interhalogen. Its shape is obtained based on the VSEPR theory. Its geometry has two types of bond angles between elements. For finding the shape of the compound the number of total number of electron pairs and number of lone pairs should be calculated.

Complete step by step answer:
According to the VSEPR theory, the shape of the molecule is predicted by the total number of electron pairs (lone pairs + bond pairs) in the valence shell of the central I(iodine) atom.
To calculate the total number of electron pairs:
$\dfrac{\text{valence electrons of central atom + number of bonded atoms}}{\text{2}}$
With the above formula: $\dfrac{7+7}{2}=7$
hence, there are 7 electron pairs.
Since there are 7 fluorine atoms joined to iodine. So, there will be a 7bond pair of electrons.
Now for calculating the number of lone pairs in the compound: -
total number of electron pairs –number of bond pairs.
Lone pairs= $7-7=0$.
Hence, in the compound, there are 0 lone pairs.
Now, for hybridization:
Depending on the number of $I-F$covalent bonds to be formed, the requisite number of electrons of the $5p-orbital$valence shell of I get unpaired and promoted to the vacant $5d-orbitals$followed by hybridization.

All interhalogen compounds of the type $X{{X}_{7}}^{'}$involve$s{{p}^{3}}{{d}^{3}}$ hybridization of the central halogen atom.

So, the hybridization is$s{{p}^{3}}{{d}^{3}}$ and it has 0 lone pairs, the geometry of$I{{F}_{7}}$ is Pentagonal bipyramidal.

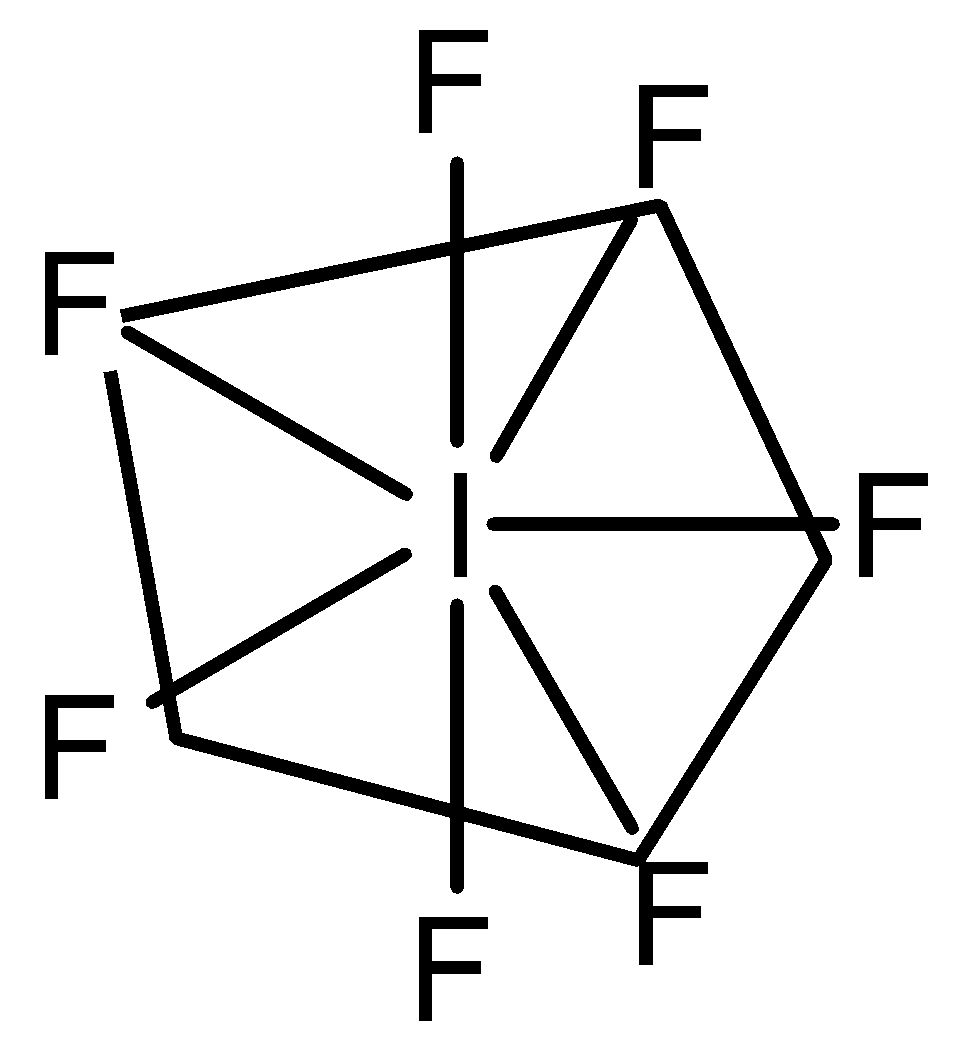
Note: Both the elements belong to the same group i.e., halogen group. The number of lone pairs should also be taken into consideration because the presence of lone pairs changes the shape and geometry completely. It has 2 bond angles, i.e., ${{90}^{\circ }}$ and ${{72}^{\circ }}$