Question

Draw the shape of five d-orbitals.

Answer 1

. Atomic orbitals:- The three-dimensional space around the atom of an element in which the electron density is maximum. It means the probability of finding an electron is maximum.

Complete step by step answer:
The transition metal ions of the outermost d-orbitals are not completely filled with electrons and hence, they can easily take and give electrons.
For d-orbitals the value of l = ${ 2 }$ , so, the value of m will be: ${ -l to +l }. { (-2,-1,0,+1,+2) }$.
As we see that there are five magnetic quantum numbers, so, the d-orbital will have five orientations. It means, five types of shapes of d-orbital in three-dimensional space.
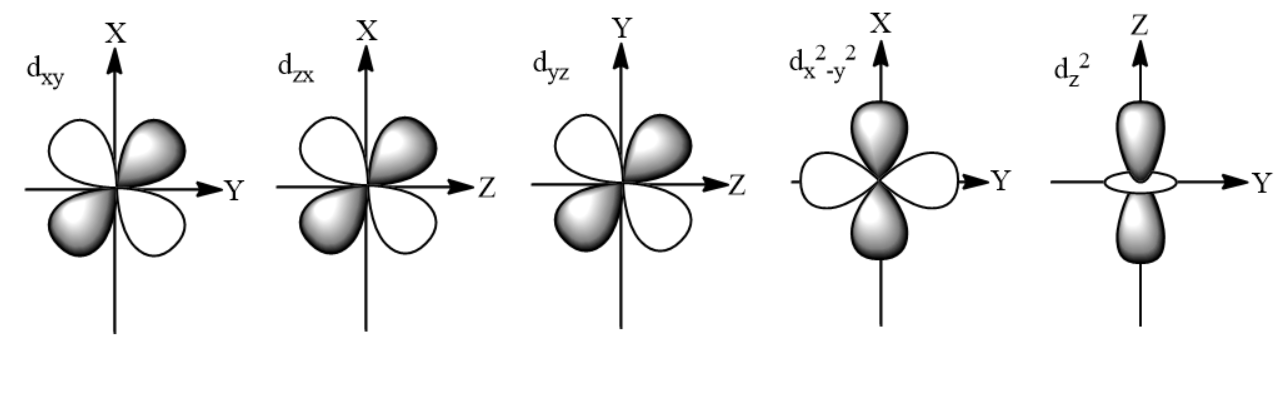
So, depending upon the axes along which or between which the electron clouds are obtained, different names and shapes are given as;
${ d }_{ xy }$ = It is of cloverleaf-like shape.
${ d }_{ yz }$ = It is of cloverleaf-like shape.
${ d }_{ xz }$ = It is of cloverleaf-like shape.
${ { d }_{ x^{ 2 } } }_{ -y^{ 2 } }$ =It is of cloverleaf-like shape.
${ { d }_{ z^{ 2 } } }$ = It is of ‘dumbbell’ and ‘doughnut’ like shape. The lobes of the ‘dumbbell' lie along the z-axis and ‘doughnut’ lies in the xy plane.
It is clear from the above names of the five d-orbitals that in which position will be assigned to them in the xyz coordinates, so the shapes are:

Additional Information:
Significance of four quantum numbers:
The principal quantum number ${ n }$ = It describes the energy and distance from the nucleus and represents the shell.
The azimuthal quantum number ${ l }$ = It describes the shape of the subshell and its orbitals.
The magnetic quantum number ${ m }$ = It describes the orientation of the orbitals in space.
The spin quantum number ${ s }$ = It describes the spin of each electron in the orbital.

Note: The possibility to make a mistake is that ${ { d }_{ x^{ 2 } } }_{ -y^{ 2 } }$ has a cloverleaf-like shape and not dumbbell as the lobes are present in the ${ xy }$ plane only.