Question

Draw the magnetic field lines of the field produced by a current carrying circular loop. Explain with reason whether the field will be stronger at a point at the centre of loop or near the circumference of the loop.

Answer 1

Using right hand thumb rule we can find the magnetic field induced by the circular current carrying loop and its direction. Also, magnetic field lines are directly proportional to the magnetic field strength.

Formula used: We can use the following formula,
Magnetic field lines $\propto$ Magnetic field strength

Complete Step by Step Solution
We know the right-hand thumb rule that will give us the direction of current and magnetic field when current induced magnetic field. It was devised by Maxwell and he suggests that If you hold a current carrying conductor in your right hand such that the thumb points out the direction of current in the conductor. Then if you curl up your fingers around the conductor, the direction the finger points at gives us the direction of the magnetic field. Thus, field lines could be drawn corresponding to what you deduced from the right-hand thumb rule.
Now consider a current carrying circular loop as below.

Holding your thumb along the direction of current $I$ we can find the magnetic field lines to be

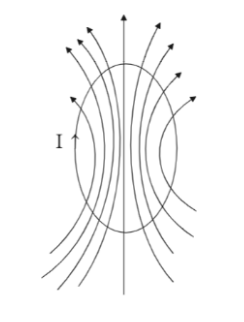
The magnetic field lines are directly proportional to the magnetic field intensity. If you observe the field lines you can see that the line is denser at the centre than at the circumference, which is why the magnetic field strength is stronger at the centre.

Note:
Alternate method
The magnetic field intensity due to current carrying circular loop at centre is given by $B = \dfrac{{{\mu _0}I}}{{2r}}$ . [where $r$ is the radius of the loop]
While the magnetic field intensity due to a current carrying circular loop at a distance $'r'$ from the radius $(r)$ is given by $B = \dfrac{{{\mu _0}I}}{{2{{({r^2} + {r^2})}^{\dfrac{3}{2}}}}}$ .
Solving for $B$ we get,
$B = \dfrac{{{\mu _0}I}}{{2{{(2{r^2})}^{\dfrac{3}{2}}}}}$
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\sqrt 2 r}}$
So comparing the values for $B$ at centre and at circumference we can see that, ${B_{centre}} > {B_{circumference}}$
Thus, the magnetic field intensity at the centre is greater than at the circumference.