Question

Draw the graphs of $\left( i \right)\,y = {x^2} - x - 6$ and $\left( {ii} \right)\,\,y = 6 - x - {x^2}$ and find zeros in each case. What do you notice?

Answer 1

Here first we will y equals to zero to find the zeros of the above quadratic equation. Using middle term splitting we can find the roots of the quadratic equation. The zeros tell us about where the graph cuts the x-axis and if we put x equals to zero we will get to know where the graph cuts the y-axis.

Complete step by step answer:
In the above question, we have
$\left( i \right)\,y = {x^2} - x - 6$
To find the zeros of the above quadratic equation, we have to put the value of y equals to zero.
${x^2} - x - 6 = 0$
$\Rightarrow {x^2} - 3x + 2x - 6 = 0$
$\Rightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0$
$\Rightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0$
So, the zeros are $x = 3, - 2$.
Also, the value of y at $x = 0$ is
$y = - 6$

$\left( {ii} \right)\,\,y = 6 - x - {x^2}$
To find the zeros of the above quadratic equation, we have to put the value of y equals to zero.
$6 - x - {x^2} = 0$
$\Rightarrow 6 + 2x - 3x - {x^2} = 0$
$\Rightarrow 2\left( {3 + x} \right) - x\left( {3 + x} \right) = 0$
$\Rightarrow \left( {3 + x} \right)\left( {2 - x} \right) = 0$
So, the zeros are $x = - 3,2$.
Also, the value of y at $x = 0$ is
$y = 6$
Therefore, the graph of above two parabolas is

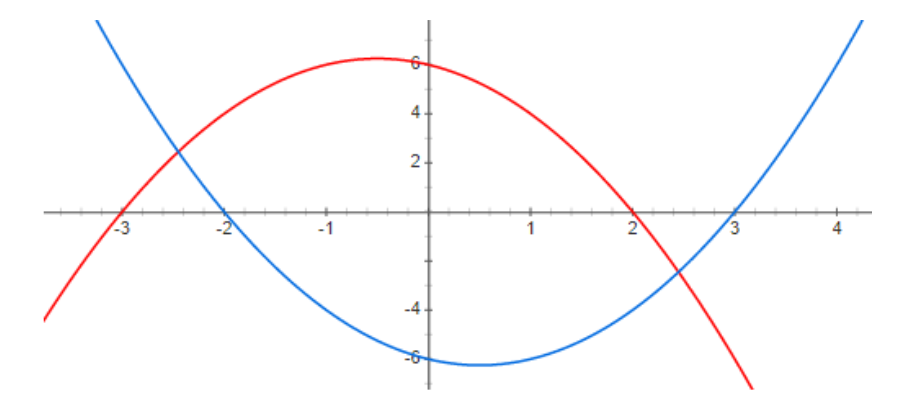
Here the red graph depicts the quadratic equation $\,y = 6 - x - {x^2}$ and the blue graph depicts the quadratic equation $y = {x^2} - x - 6$.Here we have noticed that both the graphs intersect each other at some points and also one parabola is upward and the second parabola is downward.

Note: The vertex of a parabola is the point at the intersection of the parabola and its line of symmetry. For a parabola whose equation is given in standard form, the vertex will be the minimum (lowest point) if it is a downward parabola and the maximum (highest point) if it is an upward parabola.