Question

Draw the graph (straight line) given by equation $x - 3y = 18$. If the straight line drawn passes through the points (m,-5) and (6,n), find the values of m and n?

Answer 1

The given question has two parts, first we need to plot the graph for the given equation, then it is given that two points are satisfying the line, and the coordinates are given where x and y-coordinate is missing in each point respectively, here we will use the property that if the line is passing through theses points then the points will satisfy the given line, hence will satisfy the equation.

Complete step by step solution:
On solving the first part of the question here we need to draw the graph for the straight line, in order to draw the line we know that we need at least two points, and to find those points, we will solve with the equation, on solving we get:
The given equation is $x - 3y = 18$
Assuming zero as x-coordinate we get:

$$\Rightarrow 0 - 3y = 18 \\\ \Rightarrow y = \dfrac{{ - 18}}{3} = - 6 \\\$$

Hence the first point becomes A(0,-6)
Now assuming zero as y-coordinate we get:

$$\Rightarrow x - 3(0) = 18 \\\ \Rightarrow x = 18 \\\$$

Hence the first point becomes B(18,0)
Plotting these points on graph we get:

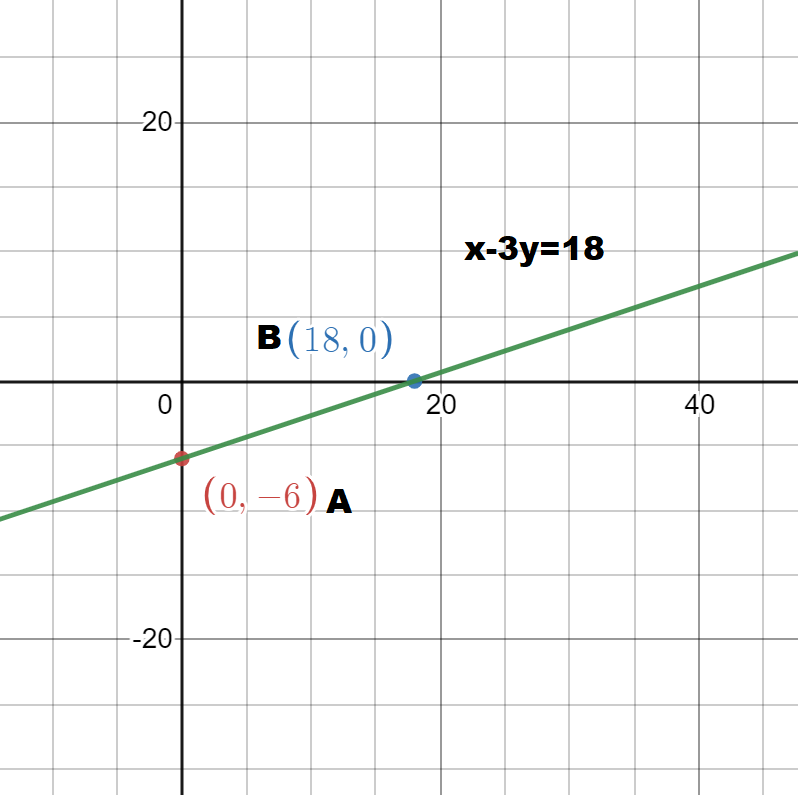
Now in the second part of the question we need to find the value of the missing coordinate, on solving we get:
For point (m,-5), putting in equation we get:

$$\Rightarrow m - 3( - 5) = 18 \\\ \Rightarrow m + 15 = 18 \\\ \Rightarrow m = 18 - 15 = 3 \\\$$

For point (6,n), putting in equation we get:

$$\Rightarrow 6 - 3(n) = 18 \\\ \Rightarrow 6 - 3n = 18 \\\ \Rightarrow 3n = 6 - 18 \\\ \Rightarrow n = \dfrac{{ - 12}}{3} = - 4 \\\$$

Here we got the values for the missing points.

Note: Here the given question needs to plot the graph of the straight line equation, and here we know that without getting at least two points for a straight line equation for a two variable we cannot plot the graph of the straight line.