Question

Draw the graph of $y = {x^2} + 3x + 2$ and use it to solve the equation ${x^2} + 2x + 4 = 0$ .

Answer 1

Hint : In this question, we need to solve the equation ${x^2} + 2x + 4 = 0$ by plotting the graph of $y = {x^2} + 3x + 2$ . Here, we will draw the graph for the given quadratic equation. To solve the second quadratic equation using the first, we will determine the roots of the second equation such that the root includes the first equation. So we will get a straight line. We can determine roots of a quadratic equation graphically by intersection of parabola with the straight line.

Complete step-by-step answer :
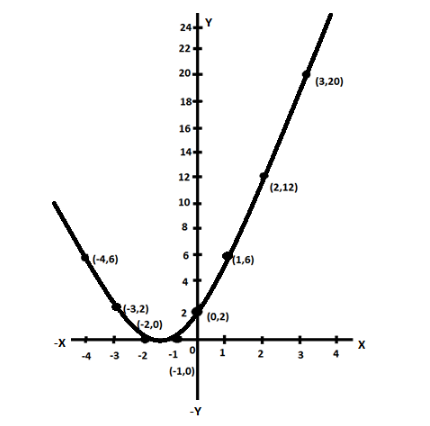
Now we will determine the points for the equation $y = {x^2} + 3x + 2$ .
Let us consider $x = 0$ , then we have,
$y = {\left( 0 \right)^2} + 3\left( 0 \right) + 2$
$y = 2$
Now, we got a point of the equation $y = {x^2} + 3x + 2$ i.e., $\left( {0,2} \right)$
Similarly, let us consider $x = 1$ , then we have,
$y = {\left( 1 \right)^2} + 3\left( 1 \right) + 2$
$y = 6$
Now, we got an another point $\left( {1,6} \right)$
Similarly substituting $x = 2,x = 3,x = - 1,x = - 2,x = - 3,x = - 4$ and solving we get the points $\left( {2,12} \right),\left( {3,20} \right),\left( { - 1,0} \right),\left( { - 2,0} \right),\left( { - 3,2} \right),\left( { - 4,6} \right)$ respectively.
Now let us plot it graphically,

Now, ${x^2} + 2x + 4 = 0$
${x^2} + 3x + 2 - x + 2 = 0$
${x^2} + 3x + 2 = x - 2$
We know that ,
$y = {x^2} + 3x + 2$
Therefore, $y = x - 2$
Thus, roots of the equation ${x^2} + 2x + 4 = 0$ are $y = {x^2} + 3x + 2$ and $y = x - 2$ .
Now, we will find the points of the equation $y = x - 2$ ,
Let, $x = 1$
$y = 1 - 2$
$y = - 1$
Therefore, the point obtained is $\left( {1, - 1} \right)$ .
Let, $x = 2$
$y = 2 - 2$
$y = 0$
Therefore, the point obtained is $\left( {2,0} \right)$ .
Similarly substituting $x = 0,x = - 1,x = - 2$ , we will obtain the points as $\left( {0, - 2} \right),\left( { - 1, - 3} \right),\left( { - 2, - 4} \right)$ .
Now plotting it in the graph,

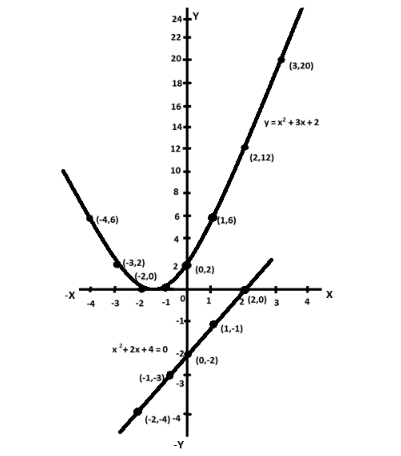
Now, from the graph, it is clear that the straight line $y = x - 2$ does not intersect the curve $y = {x^2} + 3x + 2$ . Therefore, ${x^2} + 2x + 4 = 0$ have no real roots.
So, the correct answer is “Therefore, ${x^2} + 2x + 4 = 0$ have no real roots.”.

Note : In this question, it is important to note that if the straight line intersects the parabola at two distinct points, then the coordinates of those points will be the roots of the given quadratic equation. If the straight line just touches the parabola at only one point, then the coordinate of the common point will be the single root of the quadratic equation. If the straight line doesn’t intersect or touch the parabola then the quadratic equation will have no real roots.