Question

Draw the graph of $x + 5 = 0$.

Answer 1

The given equation represents a straight line and is in the form of $x = - k$, and by the equation we can say that it is parallel to $y$-axis when the given equation is represented in a Cartesian plane, and by the equation it is clear that it passes through the point $\left( { - 5,0} \right)$, so the graph is straight line which is parallel to $y$-axis, and passes through the point $\left( { - 5,0} \right)$, that will be represented in the graph.

Complete step-by-step answer:
Given equation is $x + 5 = 0$,
This can be rewritten as, $x = - 5$,
Now firstly we will find the equation of the line that is parallel to the $y$-axis,
We know that the general form of equation of line will be,
$y = mx + c$,
And the slope of the line parallel to $y$-axis is equal to the slope of the $y$-axis which is equal to infinity, i.e.,$\dfrac{1}{0} = \infty$,
Now substituting the slope value we get,
$y = \dfrac{1}{0} \cdot x + c$,
Now taking c to other side we get,
$y - c = \dfrac{1}{0} \cdot x$,
Now cross multiplying we get,
$\left( 0 \right)y - c = x$
So, the equation of the line parallel to $y$-axis will be $x = 0$,
Now the general equation of line parallel to $y$-axis will become $x = k$, where $k$ is constant as 0 is also a constant.
So from the above derivation, the given equation $x = - 5$ is a line parallel to y-axis, and also we know that the line passed through the point $\left( { - 5,0} \right)$,
Now representing the above equation on then graph we get,

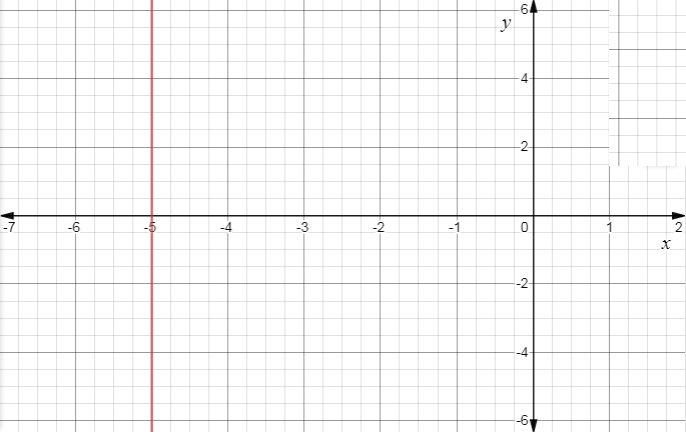
From the graph we can see that the line is parallel to $y$-axis and it passes through the point $\left( { - 5,0} \right)$.

Note:
In these type of questions, that shows that line is parallel to $x$-axis and $y$-axis we must use slope intercept formula i.e., $y = mx + c$, where m is the slope and c is the $y$-intercept of the line, and the graphs are usually represented on a Cartesian plane.