Question

Draw the graph of the function $y = |x - 1| + |x + 1|$ and discuss the continuity and differentiability of the function.

Answer 1

Here we simply draw the graph of the given function. A function is said to be continues if the curve has no missing points or breaking points in a given interval or domain. Function F(x) is said to be differentiable at a point then the differentiation of that function at that point exists. We know the definition of modulus of x.

Complete step by step answer:
We know have, |x| = \left\\{ \begin{gathered} x{\text{ }}x \geqslant 0 \\\ \- x{\text{ }}x < 0 \\\ \end{gathered} \right. this is the standard definition.
We have |x - 1| = \left\\{ \begin{gathered} x - 1{\text{ }}x > 1 \\\ \- (x - 1){\text{ }}x < 1 \\\ \end{gathered} \right. and |x + 1| = \left\\{ \begin{gathered} x + 1{\text{ }}x > - 1 \\\ \- (x + 1){\text{ }}x < \- {\text{1}} \\\ \end{gathered} \right.. ----- (1)
We have $y = |x - 1| + |x + 1|$ ---- (2)
At $x > 1$, the value of y will be
See the above definition (1) then we have,
$\Rightarrow y = x - 1 + x + 1 = 2x$ Is differentiable.
At $x < \- 1$,
By the definition (1) we will have,
$\Rightarrow y = - (x - 1) + ( - x - 1)$
$\Rightarrow y = - x + 1 - x - 1$
$\Rightarrow y = - 2x$ Is differentiable.
At $x > 1$ in $|x - 1|$ and $x > - 1$in $|x + 1|$, then the value of y will be,
$y = - (x + 1) + x + 1 = 2$ . Is differentiable.
We can see that y is differentiable,

Let’s draw the graph and check the continuity and differentiability.
At $x = 0$ in equation (2) we have $y = 2$
Similarly, at x = 1$$$$ \Rightarrow y = 2
At x = - 1$$$$ \Rightarrow y = 2
At x = 2$$$$ \Rightarrow y = 4
At x = - 2$$$$ \Rightarrow y = 4 and so on.

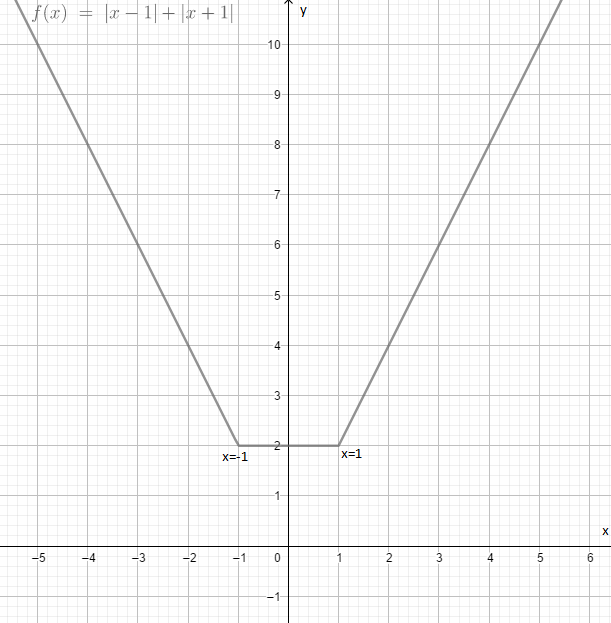
As we can see that the curve is continuous with no break points or missing points. That is $y = |x - 1| + |x + 1|$ is continuous.
But while in differentiability, at point -1 and 1 the function $y = |x - 1| + |x + 1|$ is not differentiable. Hence $y = |x - 1| + |x + 1|$ is differentiable in $R - \\{ - 1,1\\}$. Or we can also say that it is differentiable at (-1, 1)

Note: We can directly plot the graph and by observation we can tell whether it is differentiable or continuous. The function is not differentiable at $x = 1, - 1$ because the slopes at these points are different on the left and right hand side. In other wards Differentiability is defined as tangent to a curve.