Question

Draw the graph of the equation $y-2x=4$ and then answer the following.
1. Does the point (2,8) lie on the line? Is (2,8) a solution of the equation? Check by substituting (2,8) in the equation.
2. Does the point (4,2) lie one the line? is (4,2) a solution of the equation? Check algebraically also.

Answer 1

Hint: We have to draw the graph using x=0 and then y=0 to get the desired points and then we check if the given points in (i) and (ii) are satisfied by the given equation.

Complete step-by-step answer:
To draw the graph, we see possible point of x when y is put to be 0 and similarly, we see the possible points of y when x is put to be 0
Equation is $y-2x=4$………(i),
putting y=0 in equation (i) we get
$-2x=4$
$\Rightarrow x=-\dfrac{4}{2}=-2$
Similarly, putting x=0 in equation (i) we get $y=4$.

Then the possible points are $(-2,0)$ and $(0,4)$, using these values to make the graph we get graph as

Now we will proceed to answer the question given in points:
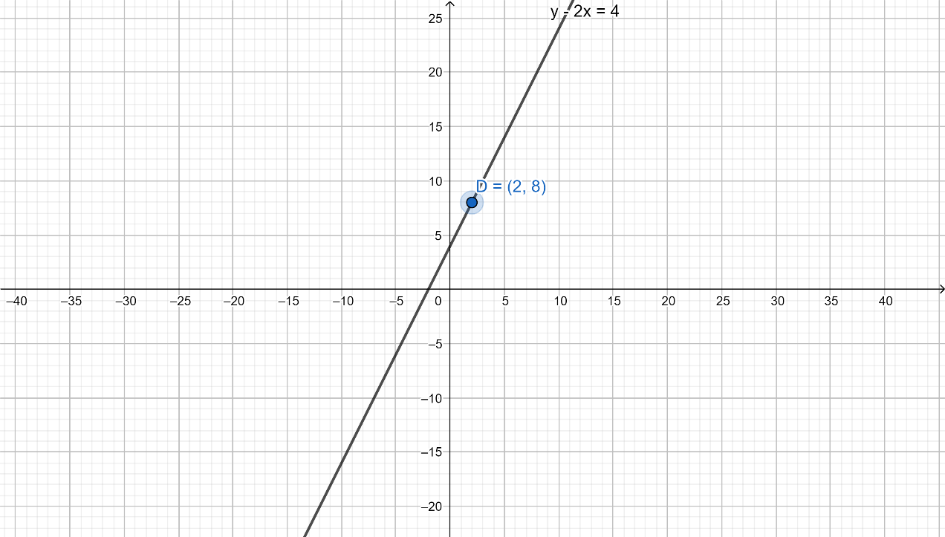
(i)To check if the point $(2,8)$ is the solution of the equation there are two methods either we check if the point $(2,8)$ lies on the line or it satisfies the given equation $y-2x=4$. The later can be done by substituting point $(2,8)$ in the equation $y-2x=4$

Putting x=2 and y=8 in left hand side of the equation $y-2x$ we get $8-4=4$, which is equal to the Right hand side of the equation, so the point $(2,8)$ satisfies the given equation $y-2x=4$. Also, because the point $(2,8)$ satisfies the given equation $y-2x=4$, so it lies on the line. Graph of it is as below:

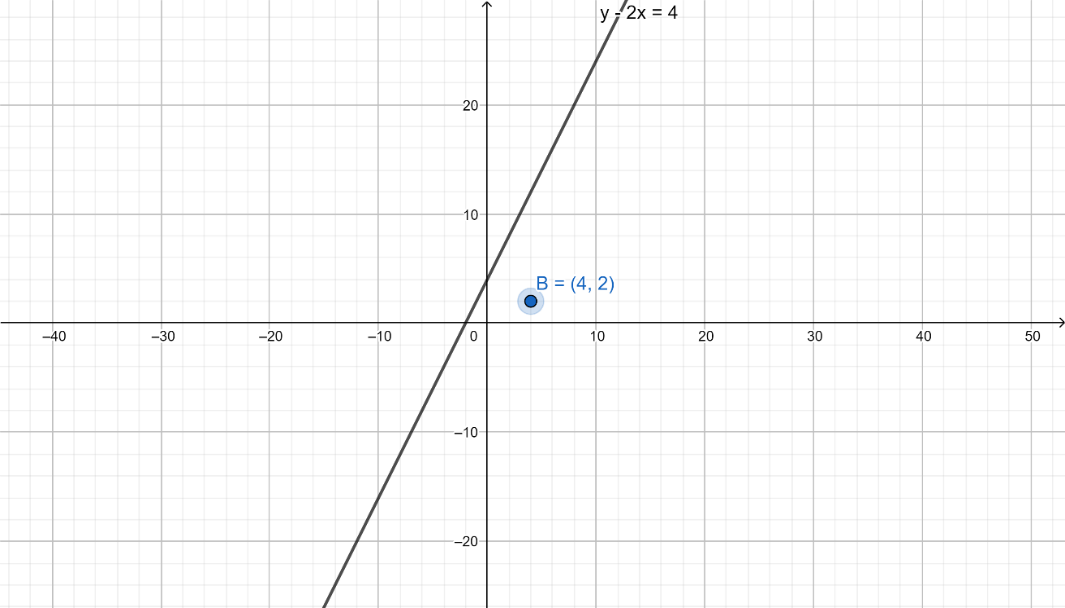
(ii) We have to do a similar procedure to check if $(4,2)$ satisfies the given equation.
Substituting x=4 and y=2 in the left hand side of the equation$y-2x=4$ we get $2-8=-6$ which is not equal to the right hand side of the given equation.
Hence, the $(4,2)$ point does not satisfy the given equation $y-2x=4$. Also, because the point $(4,2)$ does not satisfy the given equation $y-2x=4$, so it does not lie on the line. Graph of it is as below:

Note: Always verify that the given points in (i) and (ii) satisfy the given equation $y-2x=4$ by substituting the values of x and y in the L.H.S. of the equation and then proceed for graphing of the points.