Question

Draw the graph of the equation $2x + y = 6$ . Shade the region bounded by the graph and the coordinate axis, also find the area.

Answer 1

Hint : To obtain a graph of a linear equation, we first assume some points of either variable(x or y) and then calculate the value of another variable using a given linear equation and then plot these points in x y plane on joining them we will get a graph of a linear equation. Then, find the coordinate of vertices of the triangle formed by a graph of a line and coordinate axis and hence it’s required area.

Complete step-by-step answer :
Given, linear equation is: $2x + y = 6$
To plot a graph of a linear equation. We first assume some points of either of the variables and then calculate the value of another variable using the given linear equation.
Let $x = 1,$ substituting it in a given linear equation. We have,
$2(1) + y = 6 \\\ \Rightarrow 2 + y = 6 \\\ \Rightarrow y = 6 - 2 \\\ \Rightarrow y = 4 \;$
Therefore for $x = 1,$ we have y = $4$ .
Let $x = 2,$ substituting it in a given linear equation. We have,
$2(2) + y = 6 \\\ \Rightarrow 4 + y = 6 \\\ \Rightarrow y = 6 - 4 \\\ \Rightarrow y = 2 \;$
Therefore for $x = 2,$ we have y = $2$ .
Let $x = 3,$ substituting it in a given linear equation. We have,
$2(3) + y = 6 \\\ \Rightarrow 6 + y = 6 \\\ \Rightarrow y = 6 - 6 \\\ \Rightarrow y = 0 \;$
Therefore for $x = 3,$ we have y = $0$ .
Hence, from above we have a table:

x	1	2	3
y	4	2	0

Now, we will plot these points in the xy plane to find a graph of an equation $2x + y = 6$ .

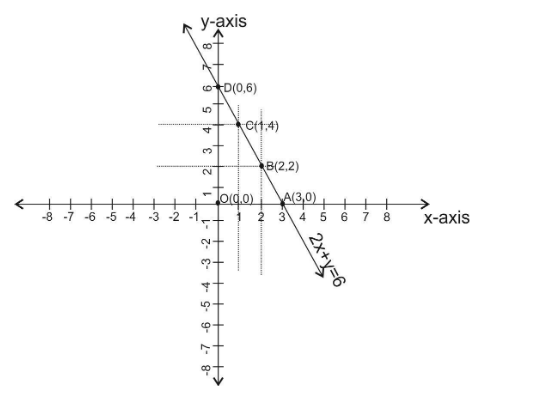
From the above graph we see that the graph of the linear equation meets the x-axis at $(3,0)$ and y-axis at $(0,6)$ .
Hence, coordinates of triangle OAB formed by graph of line and coordinate axis are given as:
$O(0,0),\,\,A(3,0)\,\,and\,\,D(0,6)$ .
Therefore, area of triangle OAB = $\dfrac{1}{2} \times OA \times OD$
$\Rightarrow ar(\Delta OAD) = \dfrac{1}{2} \times 3 \times 6 \\\ \Rightarrow ar(\Delta OAD) = 9 \;$
Hence, the area of the triangle formed by a graph of a line and coordinate axis is $9\,\,square\,\,unit.$

Note : While plotting a graph of any equation. First calculate points very carefully. If all calculated points on plotting a graph do not come on a straight line then it is a hint of mistake. As for linear equations, graphs are always a straight line.