Question
Question: Draw the graph of \(sin^2x\) and \(|sinx|\) and show the continuity and differentiability of both th...
Draw the graph of sin2x and ∣sinx∣ and show the continuity and differentiability of both the functions.
Solution
Hint: To show the continuity of a function, we should ensure that it exists at all points and there are no breaks or sharp edges on the graph of that function. To check the differentiability of a function f(x) at a point, the formula is-
limh→0hf(x+h)−f(x)existsatallvaluesofx
Complete step by step answer:
The graphs of the two functions are-
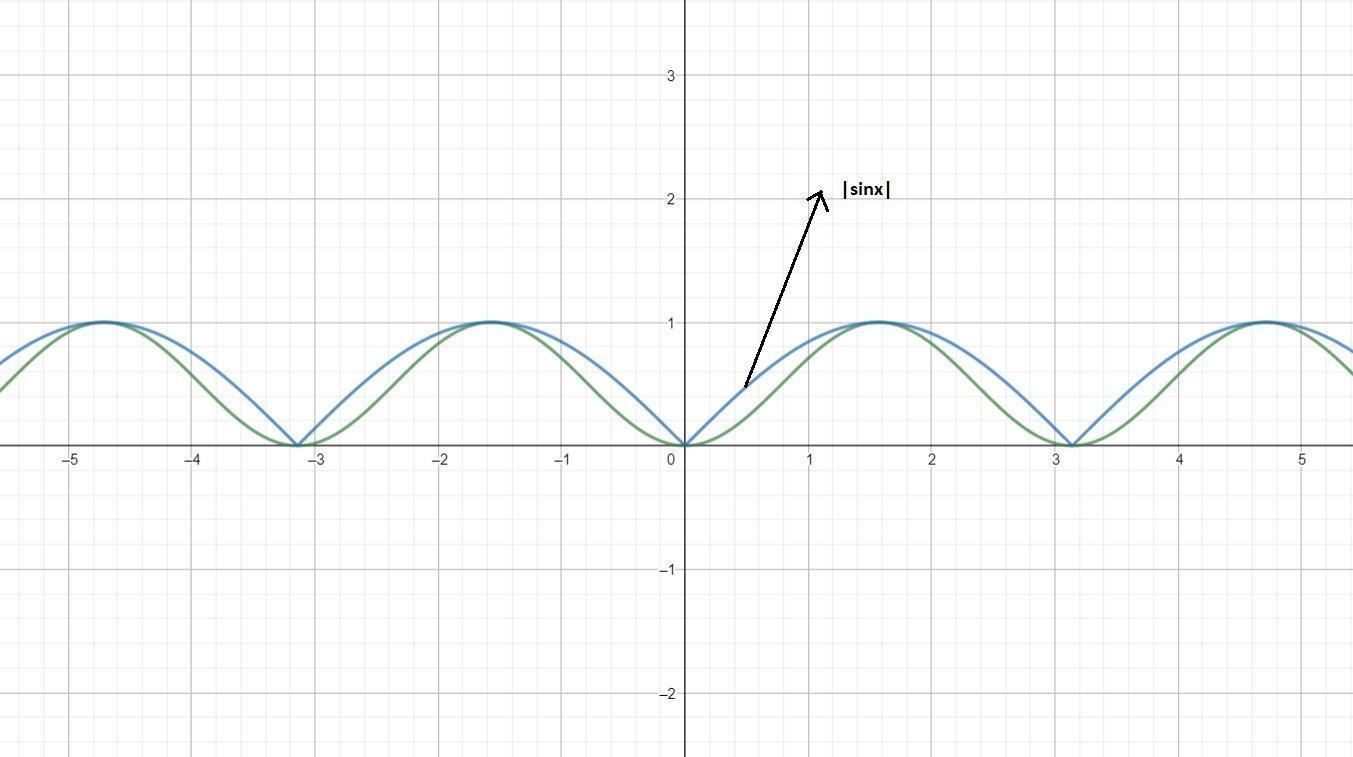
Here the the graph which is inside is sin2x and the outer one is ∣sinx∣. From the graph it is clearly visible that sin2x is smooth all along but ∣sinx∣ has a sharp curve when it touches the x-axis.
Since sin2x is smooth at all points, it is continuous and differentiable at every point.
Since ∣sinx∣ has sharp curves when it touches the x-axis, it is neither continuous nor differentiable at those points.
This is the required answer.
Note: Initially when looking at the graph, it seems that both the functions are perfectly smooth, but it is not right. Due to the presence of modulus function, ∣sinx∣ changes direction abruptly. But sin2x changes the direction in a smooth manner.
