Question

Draw the circuit diagram of $n$ resistors connected in parallel and write the equation for equivalent resistance.

Answer 1

To find the equivalent resistance of any circuit, we need to find the quantity that relates the individual resistances to the circuit as a whole (in this case, the current flowing through the resistors). The advantage of a parallel combination is that each appliance operates to its maximum intensity.

Complete step by step solution:

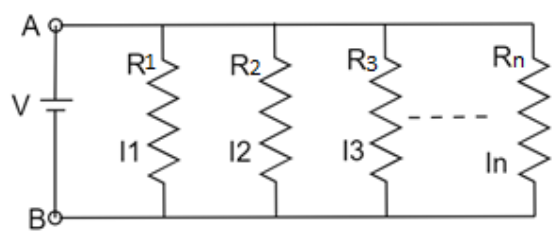
The figure shows $n$ resistances each of magnitude $R$ connected in parallel across a source of voltage $V$.
From ohm’s law, we know current flowing through a resistance is directly proportional to the voltage across it.
$\Rightarrow V=IR$(where resistance $R$ is the constant of proportionality)
Considering equivalent resistances one at a time, we can say that $V={{I}_{1}}{{R}_{1}};V={{I}_{2}}{{R}_{2}};V={{I}_{3}}{{R}_{3}};V={{I}_{n}}{{R}_{n}}$ (since potential across all resistances in parallel combination is the same)
Considering the circuit as a whole, $V=I{{\operatorname{R}}_{eq}}$
Now, since the current originating from the voltage sources gets distributed among the resistances, we can say that
$I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}+--+{{I}_{n}}$
For resistances connected in parallel across a source, we can say that the equivalent resistance expression will be
$\dfrac{V}{{{\operatorname{R}}_{eq}}}=\dfrac{V}{{{\operatorname{R}}_{1}}}+\dfrac{V}{{{\operatorname{R}}_{2}}}+\dfrac{V}{{{\operatorname{R}}_{3}}}+--+\dfrac{V}{{{\operatorname{R}}_{n}}}$
Further simplifying this expression, we can say that
$\dfrac{1}{{{\operatorname{R}}_{eq}}}=\dfrac{1}{{{\operatorname{R}}_{1}}}+\dfrac{1}{{{\operatorname{R}}_{2}}}+\dfrac{1}{{{\operatorname{R}}_{3}}}+--+\dfrac{1}{{{\operatorname{R}}_{n}}}---equation(1)$
If the resistances were of equal values, that is ${{R}_{1}}={{R}_{2}}={{R}_{3}}={{R}_{n}}=R$ , we can write the expression for equivalent resistance as
$\dfrac{V}{{{\operatorname{R}}_{eq}}}=\dfrac{V}{\operatorname{R}}+\dfrac{V}{\operatorname{R}}+\dfrac{V}{\operatorname{R}}+--+\dfrac{V}{\operatorname{R}}$

& \Rightarrow \dfrac{V}{{{\operatorname{R}}_{eq}}}=\dfrac{nV}{R} \\\ & \Rightarrow {{\operatorname{R}}_{eq}}=\dfrac{R}{n} \\\ \end{aligned}$$ This is the required equivalent resistance for $$n$$ resistances each of magnitude $$R$$ connected in parallel across a source of voltage $$V$$. Hence, the general equation for resistances connected in parallel is $$\dfrac{1}{{{\operatorname{R}}_{eq}}}=\dfrac{1}{{{\operatorname{R}}_{1}}}+\dfrac{1}{{{\operatorname{R}}_{2}}}+\dfrac{1}{{{\operatorname{R}}_{3}}}+--+\dfrac{1}{{{\operatorname{R}}_{n}}}$$ **Note:** The resistance decreases as more components are added because current finds more paths to flow through, hence more current flows from the source than would flow for any of them individually. We can also be given a question asking to find the equivalent resistance for series combination. In that case, the voltage is the physical quantity which relates the individual resistances to the circuit as a whole.