Question

Draw the block diagram of a heat engine. A steam engine delivers $5.4 \times {10^8}J$ of work per minute and services $3.6 \times {10^9}J$ of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?

Answer 1

Useful work done by the engine is equal to the difference of energy supplied to the engine and energy wasted as heat. For the determination of efficiency, we need to compute the heat rejected first. This concept becomes easier with the visualization of the block diagram.

Complete step by step answer:

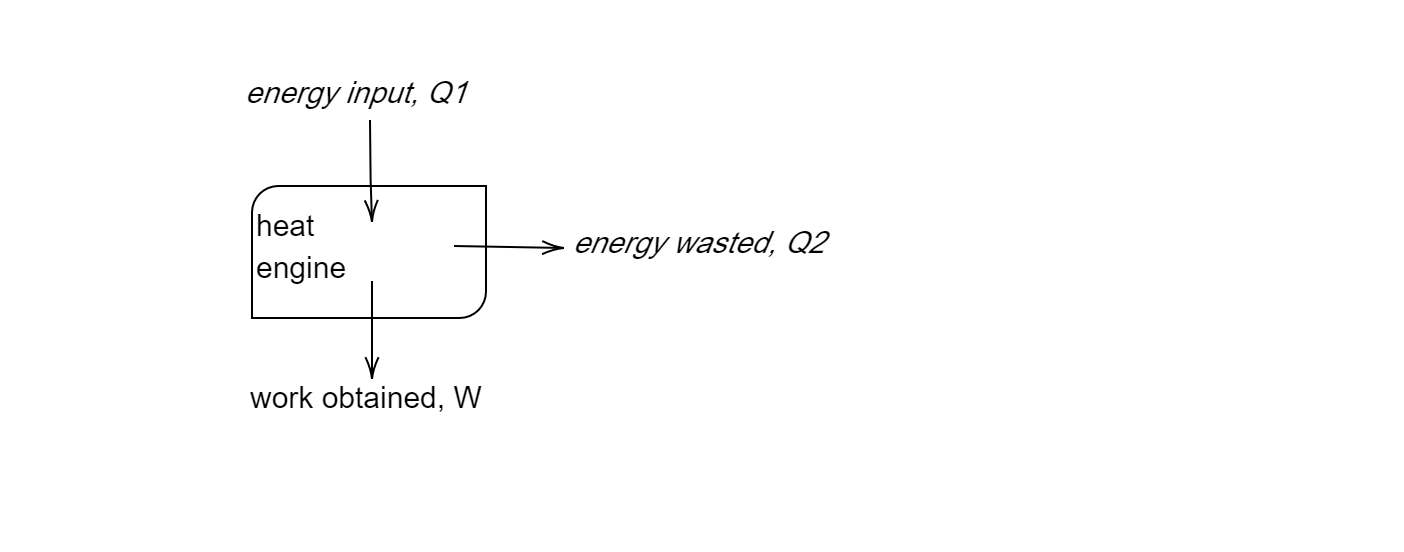
Data given to us is as follows:
Heat serviced from the boiler $({Q_1}) = 3.6 \times {10^9}J$
Work delivered by the engine $(W) = 5.4 \times {10^8}J$
Let heat rejected/wasted by the engine be ${Q_2}J$
We know that heat supplied – heat rejected = work done
Substituting the values in the above equation, ${Q_1} - {Q_2} = W$

$$\Rightarrow {Q_2} = {Q_1} - W \\\ \Rightarrow {Q_2} = 3.6 \times {10^9}J - 5.4 \times {10^8}J = (36 - 5.4) \times {10^8}J \\\ \Rightarrow {Q_2} = 30.6 \times {10^8}J \\\$$

Hence, heat rejected by the signal is $30.6 \times {10^8}J$
The efficiency of an engine is the ratio of the work obtained from the engine to the energy supplied to it.
$\Rightarrow \eta = \dfrac{W}{{{Q_1}}} = \dfrac{{5.4 \times {{10}^8}J}}{{3.6 \times {{10}^9}J}} = 0.15$
Efficiency is usually expressed as a percentage, so $\eta = 0.15 \times 100 = 15\%$

Additional Information: Heat Engine converts heat or thermal energy supplied by us to mechanical work. What differentiates heat engines from the other types of engines is that their efficiency is governed by Carnot’s theorem, that is, it cannot be more than the efficiency of a Carnot’s engine (hypothetical concept).

Note: We can approach this question using an energy conservation statement. Since we know that the energy of a system remains constant, we can say that the algebraic sum of the energy exchanges throughout the system is 0. $\sum E = 0 \Rightarrow {Q_1} + ( - {Q_2}) + ( - W) = 0$. This will again lead us to the same result.