Question

Draw phasor diagram for a series LCR circuit with alternating voltage source, determine the expression for the impedance of the circuit.

Answer 1

Hint: For getting the phasor diagram for the given conditions we will first apply the kvl across the circuit and then from the equations obtained from the kvl we will also get the expressions for the series impedance.

Complete step-by-step answer:

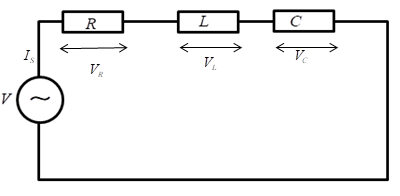
The voltage across each element in the circuit is given by
Let ${I_s} = {I_0}\sin \left( {\omega t} \right)$
Applying KVL in the above circuit
$V = {V_R} + {V_L} + {V_C}..................\left( 1 \right)$
Where
${V_R}$ is the voltage across the resistor
${V_L}$ is the voltage across inductor
${V_C}$ is the voltage across capacitor
Now according to Ohm’s law
V = IR
Now
The voltage across resistor
${V_R} = {I_s}R$
The voltage across inductor
${V_L} = {I_s}{X_L}$
${X_L}$ is the reactance of inductor
The voltage across capacitor
${V_c} = {I_s}{X_C}$
${X_C}$ is the reactance of the capacitor
Substituting these values in the equation (1)
$V = {I_s}R + {I_s}{X_L} + {I_s}{X_C}$
As we know the current leads the voltage by 90 degree in capacitor and lags by 90 degree in case of inductor.
So, taking the magnitude of above equation and assume ${X_L} > {X_C}$
$V = \sqrt {{{\left( {{I_s}R} \right)}^2} + {{\left( {{I_s}{X_L} - {I_s}{X_C}} \right)}^2}} \\\ V = {I_s}\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\\ \dfrac{V}{{{I_s}}} = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} \\\$
Let $\dfrac{V}{{{I_S}}} = Z$
$Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}}$
Z is known as impedance.
The phasor diagram of the given circuit is shown below.
The resultant vector will be obtained by adding the two vectors ${V_L}$ and ${V_C}$
Because the two vectors are 180 degree apart as shown in the below figure

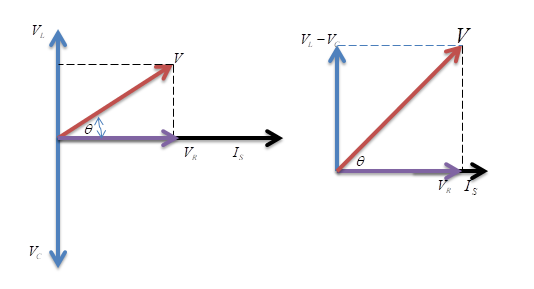
Note – While drawing the phasor diagram, the final reactive voltage must be positive in value therefore take the smallest voltage of the reactive element and subtract it from the largest voltage of the reactive element in the phasor diagram and then take the resultant using the Pythagoras theorem. The current vector is always in phase with the resistance voltage.