Question

Draw a velocity-time graph for an object in uniform motion. Show that the area under the velocity time-graph gives the displacement of the object in the given time interval.

Answer 1

Uniform motion implies a body moving with constant velocity. Displacement is the vector distance between the initial and final position of the body. Velocity-time graphs represent the movement or displacement of the body with respect to time.

Complete step-by-step answer:
Velocity refers to the rate of change of displacement of the body. Uniform velocity means that a moving body is covering the same distance for a given time period.
Let a body be moving with a constant velocity ${{v}_{0}}$.
The velocity-time graph for the body moving at uniform motion is as follows:

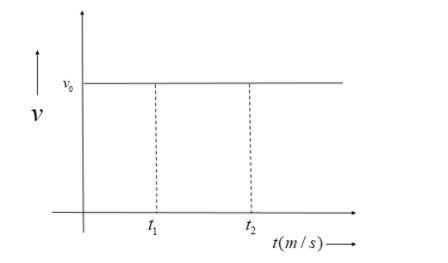
Now, let’s find the area under the graph from time ${{t}_{1}}$ to ${{t}_{2}}$:
Area = $\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{vdt}$
Here, $v={{v}_{0}}=\text{constant}$
= $\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{{{v}_{0}}dt}$
= ${{v}_{0}}\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{dt}$
Area = ${{v}_{0}}\left( {{t}_{2}}-{{t}_{1}} \right)$ ---(i)
We know, $\text{velocity}$=$\dfrac{\text{Displacement}}{time}$
$\Rightarrow Displacement=velocity\times time$
Thus, equation (i) can be written as:
Area = velocity $\times$time travelled
$\Rightarrow$ Area = displacement

Clearly, the area from any given time ${{t}_{1}}$ to time ${{t}_{2}}$ can be expressed as the product of the constant velocity and the time difference.
The product of the velocity and the time difference is nothing but displacement of the body.
Thus, the area under the velocity-time curve of a body in uniform motion is the displacement of the body.

Note: Uniform motion may not necessarily mean uniform velocity. Look for the clues as to whether the uniform motion is implied as a uniform velocity or uniform speed. Here, it is clearly mentioned that we need to draw a velocity-time graph. Hence, we can conclude that in this case, we need to take uniform motion implied as uniform velocity.