Question

Draw a rough sketch of the curves $y=\sin x\ and\ y=\cos x$, as x varies from $0\ to\ \dfrac{\pi }{2}$, and find the area of the region enclosed between them and the x – axis.

Answer 1

Hint: We will first start by drawing a graph for $y=\sin x\ and\ y=\cos x$. Then we will find the area between $x=0\ to\ x=\dfrac{\pi }{2}$ by using the integral $\int{\sin xdx}\ and\ \int{\cos xdx}$ for limits. We will refer to the graph and their point of intersection of all three curves.

Complete step-by-step answer:
Now, we know that the graph of $y=\sin x,y=\cos x\ and\ x-axis$is,

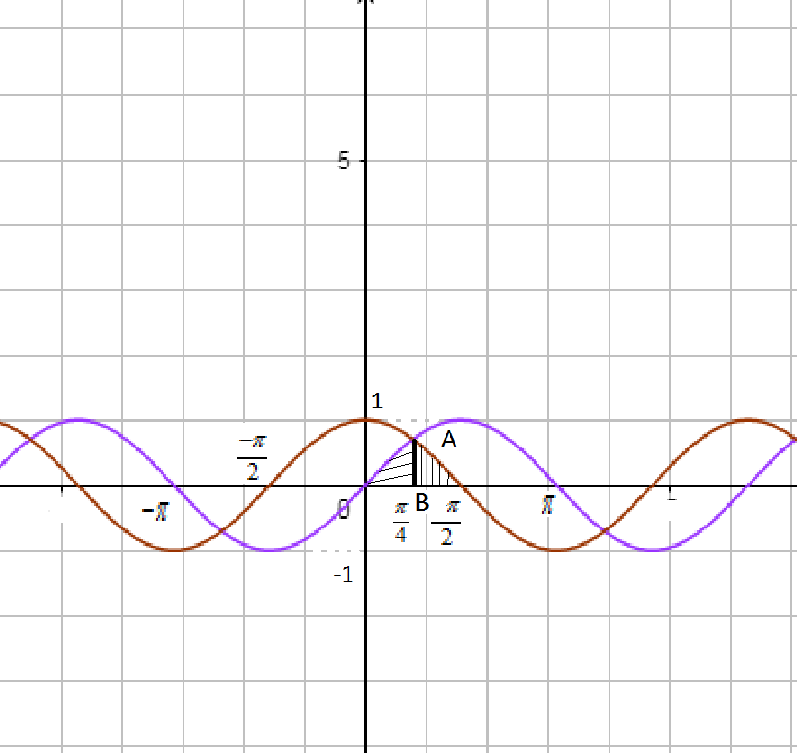
Now, we need to find the point of intersection of $y=\sin x\ and\ y=\cos x$. So we have,
$\begin{aligned} & \sin x=\cos x \\\ & \Rightarrow \dfrac{\sin x}{\cos x}=1 \\\ \end{aligned}$
Now, we know that $\dfrac{\sin x}{\cos x}=\tan x$.
$\Rightarrow \tan x=1$
Now, we know $\tan \dfrac{\pi }{4}=1$.
$\begin{aligned} & \Rightarrow \tan x=\tan \dfrac{\pi }{4} \\\ & \Rightarrow x=\dfrac{\pi }{4} \\\ \end{aligned}$
Now, to find the area of the region bounded by three curves. We have,
ar of region OAE + ar of region AEB
$\Rightarrow \int\limits_{0}^{\dfrac{\pi }{4}}{\sin xdx}+\int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}}{\cos xdx}$
Now, we know that,

& \int{\sin \theta d\theta =-\cos \theta } \\\ & \int{\cos \theta d\theta =\sin \theta } \\\ & \Rightarrow \left. -\cos x \right|_{0}^{\dfrac{\pi }{4}}+\left. \sin x \right|_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}} \\\ & \Rightarrow -\left( \cos \left( \dfrac{\pi }{4} \right)-\cos \left( 0 \right) \right)+\sin \left( \dfrac{\pi }{2} \right)-\sin \left( \dfrac{\pi }{4} \right) \\\ & \Rightarrow -\cos \dfrac{\pi }{4}+\cos \left( 0 \right)+\sin \left( \dfrac{\pi }{2} \right)-\sin \left( \dfrac{\pi }{4} \right) \\\ \end{aligned}$$ Now, we know that, $$\begin{aligned} & \sin \dfrac{\pi }{4}=\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}} \\\ & \sin \left( \dfrac{\pi }{2} \right)=\cos \left( 0 \right)=1 \\\ & \Rightarrow \dfrac{-1}{\sqrt{2}}+1+1-\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow \dfrac{-2}{\sqrt{2}}+2 \\\ & \Rightarrow 2-\sqrt{2}sq\ units \\\ \end{aligned}$$ Therefore, the area bounded by the curves is $$2-\sqrt{2}sq\ units$$. Note: It is important to note that we have to find the point of intersection of $\sin x\ and\cos x$ before integrating as the same will be used as a limit while we integrate.