Question

Draw a ray diagram to show the formation of an image for the object of height 1 cm placed at 5 cm, distance in front of a convex mirror having the radius of curvature $R=5cm$.

Answer 1

For a convex mirror, the focus and centre of curvature are on the right side of the mirror. Hence, there will be only two cases- the object is placed at infinity and the object is placed between the principal axis and infinity. A ray travelling parallel to the principal axis appears to diverge from the focus and a ray incident at the centre of curvature passes undeviated.

Complete step by step solution:

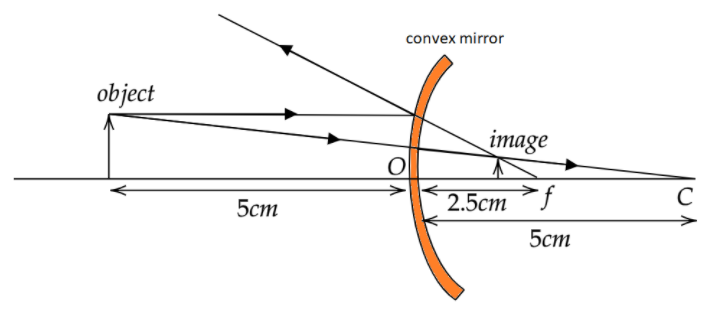
Given data in the question:
Height of the object ${{h}_{o}}$ $=1cm$
The distance of the object from the mirror (u) $=-5cm$
Focal length (f) = $\dfrac{5}{2}=2.5cm$
Now we have to first find image distance (v),
We use the formula, $\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$
Substitute values from the given data in the above formula,
$\begin{aligned} & \therefore \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u} \\\ & \therefore \dfrac{1}{v}=\dfrac{2}{5}+\dfrac{1}{5}=+\dfrac{3}{5} \\\ & \therefore v=+\dfrac{5}{3} \\\ \end{aligned}$
Therefore, the image will be formed $\dfrac{5}{3}cm$ behind the mirror.
Now let’s find the height of the image ${{h}_{i}}$ which is given by the formula,
$\dfrac{{{h}_{i}}}{{{h}_{o}}}=-\dfrac{v}{u}$
Substitute the given values in the above equation,
$\begin{aligned} & \dfrac{{{h}_{i}}}{1}=-\dfrac{\dfrac{5}{3}}{-5} \\\ & {{h}_{i}}=\dfrac{1}{3}cm \\\ \end{aligned}$

Therefore, the image will be formed of height ${{h}_{i}}$ = $\dfrac{1}{3}cm$.

Note: A ray diagram helps us trace the path that light takes to form an image of the given object. Another use of a ray diagram is to double-check the data obtained from our calculations. It helps visualize the results obtained. The image formed is diminished, that is, one-third the height of the object.