Question

Draw a pair of direct common tangents to two circles of radii 2.5cm whose centers are at 4cm apart.

Answer 1

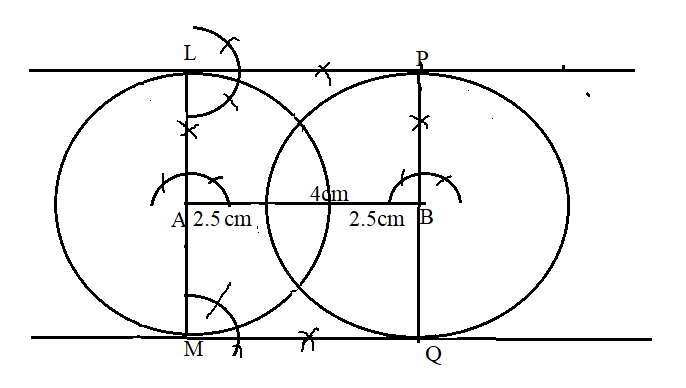
First draw a line segment of 4cm and then draw the circles of radius 2.5 cm on both the ends of the line segment. Then, construct perpendicular on the endpoints of the line segment. Draw perpendiculars on both ends of the line which is perpendicular and passing through the radius.

Complete step by step Answer:

We begin the construction by drawing a line segment of line 4cm.

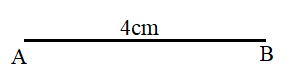
We want to construct circles whose center is 4cm apart. Since AB is a line of 4cm.
Both circles have a radius of 2.5cm.
Then, taking A as center construct a circle of radius 2.5 cm.

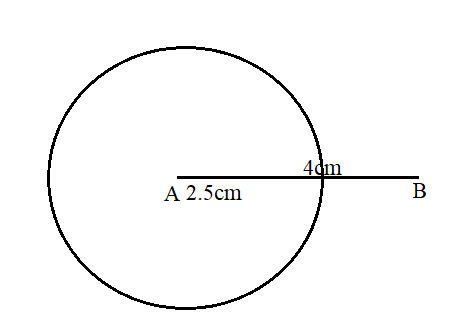
Similarly, construct a circle of radius 2.5cm by taking B as the center.

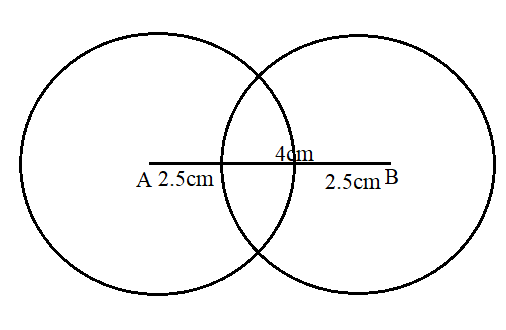
Now, we want to construct a pair of common tangents to both circles.
We know that the tangent to any circle is perpendicular to the radius of the circle.
And we want the common tangents then the radius to which the tangents are drawn should be parallel.
Hence, draw a perpendicular LM at A and PQ at B, then, LM will be parallel to PQ

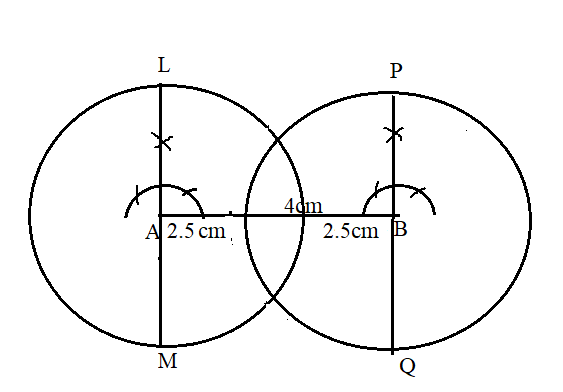
We will now draw tangents passing trough points L and P, and one tangent passing through M and Q.
Draw a perpendicular to LM at point L and perpendicular to PQ at line Q.
And join the lines LP and MQ which are a pair of tangents to the two circles.

Note: A tangent is a line that touches the circle at one point. The tangent is perpendicular to the radius. While doing construction, make sure the pencil is sharp and the compass is kept properly to avoid errors.