Question

Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.

Answer 1

A conical pendulum consists of a Bob revolving in a horizontal circle with a constant speed at the end of a string. The string makes a constant angle with the vertical so it describes a cone whereas the bob of the pendulum describes a horizontal circle.

Complete answer:
The force required to keep an object moving in a circular path is known as centripetal force.This force will be always directed inward towards the centre of rotation.

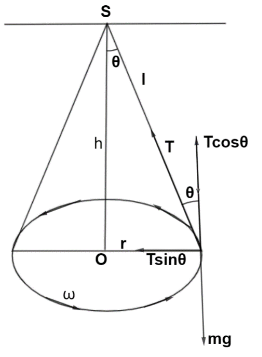
Were, $S$: rigid support, $T$: tension in the string, $l$: length of string, $h$: height of support from bob, $v$: velocity of bob and $r$: radius of horizontal circle.

Consider a bob of mass ‘m’ tied to one end of a string of length ‘l’ and the other end is fixed to a rigid support. Let the bob be displaced from its mean position and whirled around a horizontal circle of radius ‘r’ with constant angular velocity $\omega$ , then the bob performs uniform circular motion. During the motion, a string is inclined to the vertical at an angle $\theta$ as shown in the above figure.

In the displaced position P, there are two forces acting on the bob. The weight mg acting vertically downwards and the tension T acting upward along the string. The tension (T) acting in the string can be resolved into two components that are $T\cos \theta$ acting vertically upwards. $T\sin \theta$ acting horizontally towards the centre of the circle. Vertical component $T\cos \theta$ balances the weight and the horizontal component $T\sin \theta$ provides the necessary centripetal force.

The force required to keep an object moving in a circular path is known as centripetal force.This force will be always directed inward towards the centre of rotation. This necessary centripetal acceleration required for the motion of the conical pendulum is provided by the x component of tension which is the horizontal component.
$T\cos \theta = mg - - - - (1)$
$\Rightarrow T\sin \theta = \dfrac{{m{v^2}}}{r} = mr{\omega ^2} - - - - (2)$
Dividing equation (2) by (1) we get,
$\tan \theta = \dfrac{{{v^2}}}{{rg}} - - - - (3)$

Therefore, the angle made by the string with the vertical is $\theta = {\tan ^{ - 1}}\left( {\dfrac{{{v^2}}}{{rg}}} \right)$
Also, from the equation (3)
${v^2} = rg\tan \theta$
$\Rightarrow v = \sqrt {rg\tan \theta }$
The time period,
$T = \dfrac{{2\pi r}}{v} = \dfrac{{2\pi r}}{{\sqrt {rg\tan \theta } }} \\\ \Rightarrow T= 2\pi \sqrt {\dfrac{r}{{g\tan \theta }}}$
It can be seen that $r = l\sin \theta$
$T= 2\pi \sqrt {\dfrac{{l\sin \theta }}{{g\tan \theta }}}$
$\therefore T = 2\pi \sqrt {\dfrac{{l\cos \theta }}{g}}$
The time period of conical pendulum is $T = 2\pi \sqrt {\dfrac{{l\cos \theta }}{g}}$.

Note: The force required to keep an object moving in a circular path is known as centripetal force. This force will be always directed inward towards the centre of rotation.Don't confuse centripetal force with centrifugal force. Centrifugal force is the force felt by an object moving on a circular path which acts away from the centre.