Question

Draw a graph to show the variation of the angle of deviation $(\delta )$ with that the angle of incidence $(i)$ for a monochromatic ray of light passing through a glass prism of refracting angle $(A)$ then deduce the relation: $\mu = \dfrac{{\sin (\dfrac{{A + {\delta _m}}}{2})}}{{\sin \dfrac{A}{2}}}$

Answer 1

A transparent item with two triangular ends and three rectangular sides is known as a glass prism. The refraction of light in a glass prism differs from the refraction of light in a glass slab. This is because the incident beam of light in a glass prism is not parallel to the emergent ray of light. The bending of light which occurs when it travels from one medium to another is called refraction. For example, when a ray of light passes through a glass prism, refraction happens both when it enters and exits the prism.

Complete step by step answer:
The angle at which the emergent ray deviates from the incoming light's direction is known as the angle of deviation. As the angle of incidence increases, the angle of deviation falls until it reaches a minimal value. As the angle of incidence increases, the angle of deviation increases too.

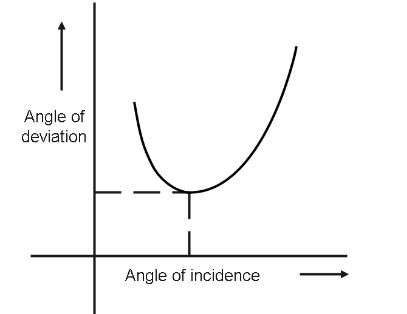
The angle of deviation is minimum for the symmetrical path of light ray through prism.

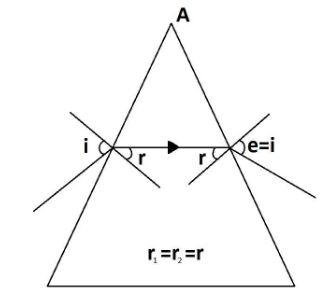
Incidence angle = emergence angle
$i = e$ or ${r_1} = {r_2} = r$
Hence,
$A + {\delta _m } = i + i = 2i \\\ \Rightarrow i = \dfrac{A + {\delta _m }}{2} \\\ \Rightarrow A = {r_1} + {r_2} = 2r \\\ \Rightarrow r = \dfrac{A}{2}$
And $\mu = \dfrac{{\sin i}}{{\sin {r}}}$
After putting the values of $i$ and $r$ in the above equation we get,
$\therefore \mu = \dfrac{{\sin (\dfrac{{A + {\delta _m}}}{2})}}{{\sin \dfrac{A}{2}}}$

Note: As we have seen, a light beam touching one face of a triangular glass prism is refracted twice and emerges from the other face. The angle of deviation is the angle formed by the emerging and incident rays. The refracting angle of the prism is the angle formed by the two refracting faces.