Question

Draw a diagram to show the conservation of mechanical energy in case of a free-falling body.

Answer 1

In this question, use the law of conservation of energy that is the energy of the system remains constant, to check the mechanical energy is constant in the whole path. If it remains constant then we can say that the mechanical energy is conserved in case of a free-falling body.

Complete step by step solution:
From the diagram as shown below, we have three points A, B, C, where A is the highest point, B is somewhere in between the path, and the point C is just before hitting the ground.
Consider the diagram of the conservation of mechanical energy in case of a free-falling body as,

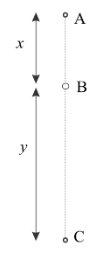
According to the Law of conservation of energy, the energy neither be created nor be destroyed, that is the total energy remains constant.
We can write the formula for the potential energy as,
$P.E = mgh$
Where, $m$is the mass, $g$is the acceleration due to gravity and $h$is the height.
For point A, first we will calculate the potential energy that is $P.E = mgh$
Where,$h = x + y$, so the potential energy can be written as,
$P.E = mg\left( {x + y} \right)$
We can write the formula for the kinetic energy as,
$K.E = \dfrac{1}{2}m{u^2}$
Where, $m$is the mass and the velocity of the object is $u$.
The point A is the highest point where the object stops, so the velocity$\left( u \right)$is zero, so the kinetic energy will be calculated as,
$K.E = \dfrac{1}{2}m{u^2} \\\ K.E = \dfrac{1}{2}m{\left( 0 \right)^2} \\\ K.E = 0 \\\$
The mechanical energy of the system is the sum of the potential energy and the kinetic energy of the system. It can be written as,
$M.E = P.E + K.E$
Substitute the given values in the in the above equation,
$M.E = P.E + K.E \\\ = mg\left( {x + y} \right) + 0 \\\ = mg\left( {x + y} \right) \\\$
Hence, total mechanical energy for point A is $mg\left( {x + y} \right)$ that is there is only potential energy.
For point C, when the body just touches the ground height will be zero, so the potential energy will be zero. So, the potential energy of the system is converted into kinetic energy.
The kinetic energy or the total mechanical energy can be written as,
$K.E = \dfrac{1}{2}m{V^2}$
Where, $V$is the velocity at point C.

To calculate the velocity, we can use the equation of motion under uniform acceleration. So for the path A to C, at point A initial velocity$\left( u \right)$zero, acceleration$\left( a \right)$for the whole path is gravity$\left( g \right)$and the total displacement is $\left( {S = x + y} \right)$.
${V^2} = {u^2} + 2aS \\\ {V^2} = 0 + 2g\left( {x + y} \right) \\\ {V^2} = 2g\left( {x + y} \right) \\\$
Substitute the value of the velocity in the equation of the kinetic energy at C as,
$KE = \dfrac{1}{2}m{V^2} \\\ = \dfrac{1}{2}m \times 2g\left( {x + y} \right) \\\ = mg\left( {x + y} \right) \\\$
Hence, total mechanical energy at point C is $mg\left( {x + y} \right)$.
The total mechanical energy at point A and C is the same, so we can say that the mechanical energy is conserved in the whole path.

Note:
This derivation is valid when there is no resistance in air or any other external forces otherwise all the energy will be wasted. There can be another question in a student's mind that what will happen once the body hits the ground so when the body will hit the ground the energy will be converted into heat, friction, light energy.