Question

Draw 3 equipotential surfaces corresponding to a field that uniformly increased in magnitude but remains constant along positive Z-direction. How are these surfaces different from that of a constant electric field along Z-direction?

Answer 1

Hint : The three equipotential surfaces at the location placed should all be in the same potential. For a given potential, the electric field is inversely proportional to the distance of the point of interest to a reference point.

Formula used: In this solution we will be using the following formula;
$E = \dfrac{V}{d}$ where $E$ is the electric field at a point, $V$ is the electric potential at a point with reference to another point, and $d$ is the distance between the reference point, and the point of interest.

Complete step by step answer:

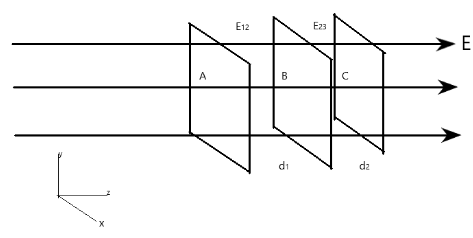
To draw equipotential surfaces, we note that equipotential surfaces are surfaces with equal potential, i.e. there are no potential differences between them.
Now imagine three surfaces on the x-y plane perpendicular to the electric field in the z axis, as shown in figure. In average form, the electric field can be given as
$E = \dfrac{V}{d}$ where $V$ is the electric potential at a point with reference to another point, and $d$ is the distance between the reference point, and the point of interest.
Now, say the surface A is at a potential V, then surface B will be at a potential
${V_B} = {E_{12}}{d_{12}}$ with respect to A, and surface C will be at
${V_C} = {E_{23}}{d_{23}}$ with respect to B.
Now, since they are equipotential surfaces, then
$V = {V_B} = {V_C}$
Then by equating the expression,
${E_{12}}{d_{12}} = {E_{23}}{d_{23}}$
$\Rightarrow {d_{23}} = \dfrac{{{E_{12}}{d_{12}}}}{{{E_{23}}}}$
Hence, since ${E_{23}} > {E_{12}}$ (because the electric field increases along the z axis), then
${d_{23}} < {d_{12}}$
This means that the distance between the surfaces decreases. Hence BC should be drawn closer together than AB.
If the electric field was constant, then ${d_{23}} = {d_{12}}$ hence, they would be equally spaced apart.

Note:
Note that the equation $E = \dfrac{V}{d}$ is just the constant form which shows the relation between the quantities and thus enough to solve our problem. However, in actuality, since the electric field changes the equation should be given as
${V_B} = \int_0^{{d_1}} {Edz}$ . The electric field ${E_{12}}$ and ${E_{23}}$ are more or less averages.