Question
Question: Domain of \(f(x) = log(\sqrt{10(3^{x-2})-9^{x-1}-1}+\sqrt{sin^{-1}(2-x)}\) is \([a,b]\) then sum a+b...
Domain of f(x)=log(10(3x−2)−9x−1−1+sin−1(2−x) is [a,b] then sum a+b is equal to _____.
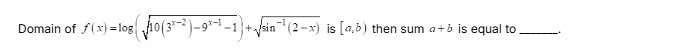
3
Solution
The given function is f(x)=log(10(3x−2)−9x−1−1+sin−1(2−x).
For the function to be defined, the following conditions must be met:
-
The argument of the logarithm must be strictly positive: 10(3x−2)−9x−1−1+sin−1(2−x)>0.
-
The arguments of the square roots must be non-negative:
a) 10(3x−2)−9x−1−1≥0 b) sin−1(2−x)≥0
-
The argument of the inverse sine function must be in its domain, which is [−1,1]: −1≤2−x≤1.
Let's analyze each condition.
Condition 2a: 10(3x−2)−9x−1−1≥0
10⋅323x−99x−1≥0
910⋅3x−9(3x)2−1≥0
Multiply by 9: 10⋅3x−(3x)2−9≥0
Let y=3x. Since 3x>0 for all real x, y>0.
−y2+10y−9≥0
y2−10y+9≤0
Factor the quadratic: (y−1)(y−9)≤0
This inequality holds when 1≤y≤9.
Substitute back y=3x: 1≤3x≤9
30≤3x≤32
Since the base 3 is greater than 1, the inequality holds for the exponents: 0≤x≤2.
Condition 2b: sin−1(2−x)≥0
The range of sin−1(u) is [−2π,2π]. sin−1(u)≥0 if and only if u∈[0,1].
So, 0≤2−x≤1.
0≤2−x⟹x≤2.
2−x≤1⟹2−1≤x⟹1≤x.
So, 1≤x≤2.
Condition 3: −1≤2−x≤1
−1≤2−x⟹x≤2−(−1)⟹x≤3.
2−x≤1⟹2−1≤x⟹1≤x.
So, 1≤x≤3.
For the square roots to be defined and the argument of sin−1 to be in the correct range, x must satisfy conditions 2a, 2b, and 3. The intersection of the intervals from these conditions is:
[0,2]∩[1,2]∩[1,3]=[1,2].
So, for the terms under the square roots to be non-negative and the argument of sin−1 to be valid, we must have x∈[1,2].
Now consider condition 1: 10(3x−2)−9x−1−1+sin−1(2−x)>0.
Let A(x)=10(3x−2)−9x−1−1 and B(x)=sin−1(2−x).
For x∈[1,2], we know A(x)≥0 and B(x)≥0.
The sum A(x)+B(x) is non-negative for x∈[1,2].
For the logarithm to be defined, the sum must be strictly positive.
The sum is zero if and only if both terms are zero simultaneously: A(x)=0 and B(x)=0, which means A(x)=0 and B(x)=0.
A(x)=0⟹10(3x−2)−9x−1−1=0. We found that this equation holds for x=2.
B(x)=0⟹sin−1(2−x)=0. This happens when 2−x=sin(0)=0, which means x=2.
Both A(x)=0 and B(x)=0 occur simultaneously only at x=2.
At x=2, the argument of the logarithm is 0+0=0, which is not strictly positive.
Therefore, x=2 must be excluded from the domain.
For x∈[1,2), we have 1≤x<2.
For x∈[1,2), A(x)=−(3x−1)(3x−9). Since 3≤3x<9, 3x−1>0 and 3x−9<0. Thus A(x)=−(+)(−)=+>0. So A(x)>0.
For x∈[1,2), 0<2−x≤1. So B(x)=sin−1(2−x)∈(0,π/2]. Thus B(x)>0. So B(x)>0.
For x∈[1,2), both terms under the square root are positive, so their sum is positive.
The domain of the function is the set of x values satisfying x∈[1,2] and A(x)+B(x)>0.
This is the interval [1,2] excluding the point where the sum is zero, which is x=2.
So the domain is [1,2).
The question states that the domain is [a,b]. This implies a closed interval. However, our derivation leads to an open interval at the upper bound. Assuming the question intended the domain to be a closed interval or there's a specific context where the domain is interpreted as such, we proceed with the derived interval [1,2) and check if the boundary points are included or excluded based on the conditions.
Let's reconsider the conditions and the wording of the question. The question explicitly states the domain is [a,b]. This suggests that both endpoints are included.
If the domain is [a,b], then we must have a=1 and b=2.
Let's check if the function is defined at x=1 and x=2.
At x=1:
A(1)=10(31−2)−91−1−1=10(3−1)−90−1=10/3−1−1=10/3−2=4/3.
B(1)=sin−1(2−1)=sin−1(1)=π/2.
Argument of log is 4/3+π/2>0. So x=1 is in the domain.
At x=2:
A(2)=10(32−2)−92−1−1=10(30)−91−1=10(1)−9−1=10−9−1=0.
B(2)=sin−1(2−2)=sin−1(0)=0.
Argument of log is 0+0=0.
Since the argument of the logarithm must be strictly positive, x=2 is NOT in the domain.
Our derived domain is [1,2). This contradicts the statement that the domain is [a,b].
There might be a typo in the question, either in the function definition or the stated form of the domain.
Assuming the function is correctly given and the domain is indeed of the form [a,b], it implies that the argument of the logarithm is always strictly positive for x∈[a,b], and the conditions for the square roots and inverse sine are met within this interval.
If we strictly follow the conditions for the domain of the given function, the domain is [1,2).
If we assume the question's statement about the domain being [a,b] is correct, and our calculations for the conditions are correct, then there is a contradiction.
Let's assume there is a typo in the function, and the domain is indeed [a,b]. The calculation of the valid range for x based on the arguments of square roots and inverse sine gives [1,2]. If the domain is [a,b], and this is the domain where the function is defined, then it must be [1,2]. But at x=2, the argument of the logarithm is 0.
Given the problem structure asking for a+b from the domain [a,b], it strongly suggests that the domain is a closed interval. The only way our derived domain [1,2) becomes a closed interval [1,2] is if the argument of the logarithm is strictly positive for all x∈[1,2], including x=2. This is not the case.
However, in some contexts, the domain might refer to the values of x for which the expression is real, even if the logarithm is not defined (e.g., if the argument is 0). But the standard definition of the domain of log(u) requires u>0.
Assuming the question has a flaw and the intended domain for calculating a+b is the interval where the terms under the square roots are defined and non-negative, which is [1,2], we set a=1 and b=2. The sum a+b=1+2=3.
