Question

Distance of the point (2, 1) from the line 3x - y - 6 = 0 along a line x - y + 2 = 0 is

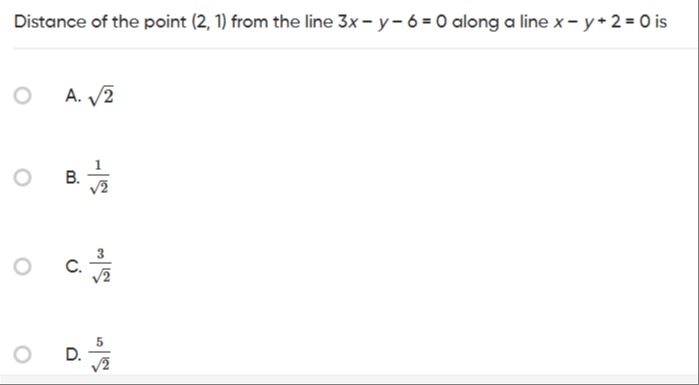
• A. $\sqrt{2}$
• B. $\frac{1}{\sqrt{2}}$
• C. $\frac{3}{\sqrt{2}}$
• D. $\frac{5}{\sqrt{2}}$

Answer 1

Answer: (B)

$\frac{1}{\sqrt{2}}$

Answer 2

1. Direction of the line of measurement: The line $x - y + 2 = 0$ has a slope of 1. A direction vector for this line is $(1, 1)$.
2. Parametric equation of the line through the point: The line passing through point (2, 1) and parallel to $x - y + 2 = 0$ can be represented parametrically as: $x = 2 + t$, $y = 1 + t$.
3. Point of intersection: Substitute into $3x - y - 6 = 0$: $3(2 + t) - (1 + t) - 6 = 0 \Rightarrow 6 + 3t - 1 - t - 6 = 0 \Rightarrow 2t - 1 = 0 \Rightarrow t = \frac{1}{2}$.
4. Coordinates of intersection point: $x = 2 + \frac{1}{2} = \frac{5}{2}$, $y = 1 + \frac{1}{2} = \frac{3}{2}$. The intersection point is $(\frac{5}{2}, \frac{3}{2})$.
5. Distance between the point and intersection point: $d = \sqrt{(\frac{5}{2} - 2)^2 + (\frac{3}{2} - 1)^2} = \sqrt{(\frac{1}{2})^2 + (\frac{1}{2})^2} = \sqrt{\frac{1}{4} + \frac{1}{4}} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}}$.