Question

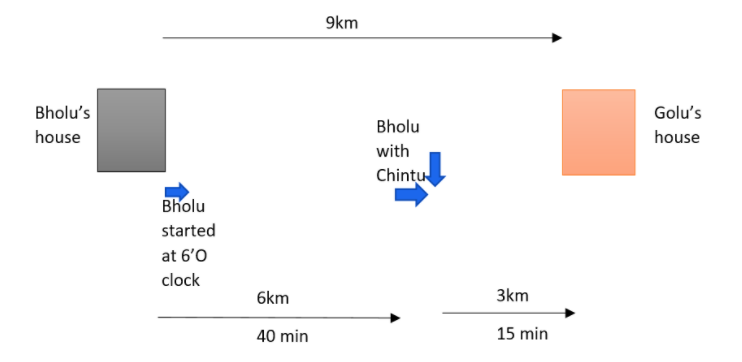
Distance between Golu’s and Bholu’s house is given as $9km$. Bholu has to attend Golu’s birthday party at $7$ o’clock. He started from his home at $6$ o’clock on his bicycle and covered a distance of $6km$ in $40\min$. At that point he met Chintu and he spoke to him for $5\min$and reached Golu’s birthday party at $7$ o’clock. With what speed did he take to complete the second part of the journey? Calculate his average speed for the entire journey to compete.

Answer 1

The speed at which Bholu covered the second part of journey can be calculated by taking the ratio of the distance left to reach Golu’s house to the time left for the travel. In order to calculate the average speed, the total distance covered in the full journey is divided by the total time taken to complete the whole journey. These all may help you to solve this question.

Complete answer:
The speed at which the Bholu covered the second part of the journey is calculated by the equation,
$s=\dfrac{\text{distance left to reach Golu }\\!\\!'\\!\\!\text{ s house}}{\text{time left}}$
The distance left to reach the house of Golu will be,
$d=9-6km=3km$
The time left will be,
$t=1hr-45\min =\dfrac{1}{4}hr$
Therefore the speed of Bholu in the second journey will be,
$s=\dfrac{3km}{\dfrac{1}{4}h}=12km{{h}^{-1}}$
Now let us calculate the average speed of the boy. The average speed will be the total distance covered in the full journey divided by the total time taken to complete the whole journey. Therefore we can write that,
${{S}_{avg}}=\dfrac{\text{total distance travelled}}{\text{total time taken}}$
The total distance travelled is given as,
${{d}_{t}}=9km$
The total time taken for the complete journey will be,
$t=1h$
Therefore the average speed will be given as,
${{S}_{avg}}=\dfrac{9km}{1h}=9km{{h}^{-1}}$
Therefore the correct answer for the question has been obtained.

Note:
Average speed is a scalar quantity. This means that the quantity does not depend on the direction of the travel. Average speed is the rate at which a journey takes place. The speed will vary from time to time. Therefore the average speed becomes important to have an idea about the rate at which the journey is completed.