Question

Distance between centres of two stars is $10a$. The masses of these stars are $M$ and $16M$and their radii are $a$and$2a$, respectively. A body is fired straight from the surface of the large star towards the smaller star. What should be its minimum initial speed to reach the surface of the smaller star?

Answer 1

We now that when a body is thrown from one surface to another surface, it is attracted towards both the surface due to their gravitational forces at some point between these two surfaces, the body experiences equilibrium condition when it is under equal gravitational force of both the surface. Here, we will use this concept first to find the distance of the body from surfaces of both stars to point at which the body is under equal influence of forces of both the stars which act in opposite directions. After that, we will use the law of conservation of energy to find the body's minimum initial speed to reach the surface of the smaller star.

Formulas used:
$F = \dfrac{{GMm}}{{{r^2}}}$ ,
where, $F$ is attractive force, $G$ is the gravitational constant, $M$ and $m$ are two masses separated by distance $r$ and $r$ is the distance between both masses
$E = - \dfrac{{GMm}}{{{r^{}}}}$,
where, $E$ is gravitational potential energy, $G$ is the gravitational constant, $M$ and $m$ are two masses separated by distance $r$ and $r$ is the distance between both masses
$K.E. = \dfrac{1}{2}m{v^2}$,
where, $K.E.$ is kinetic energy, $m$ is mass of the body and $v$ is velocity of the body

Complete step by step answer:

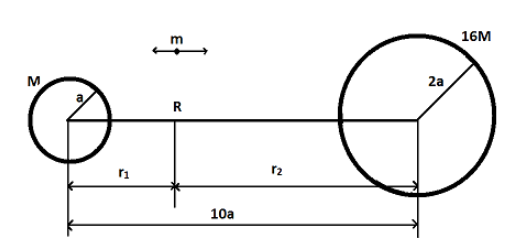
From the diagram, Let as consider that at point R, the body with mass $m$ experiences equilibrium condition when it is under equal gravitational force of both the surfaces. Attractive force of smaller star is given by $\dfrac{{GMm}}{{{r_1}^2}}$and that of the bigger star is given by $\dfrac{{16GMm}}{{{r_2}^2}}$
Now, at point R,
$\dfrac{{GMm}}{{{r_1}^2}} = \dfrac{{16GMm}}{{{r_2}^2}} \\\ \Rightarrow \left( {\dfrac{{{r_2}^2}}{{{r_1}^2}}} \right) = 16 \\\ \Rightarrow {r_2} = 4{r_1} \\\$
The total distance between the stars is given as $10a$
$\Rightarrow {r_1} + {r_2} = 10a \\\ \Rightarrow {r_1} + 4{r_1} = 10a \\\ \Rightarrow 5{r_1} = 10a \\\ \Rightarrow {r_1} = 2a \\\ \Rightarrow {r_2} = 8a \\\$
Now we will use the energy conservation between the surface of the bigger star and point R.

$$\Rightarrow K.E{._{surface}} + P.E{._{surface}} = K.E{._R} + P.E{._R} \\\ \Rightarrow \dfrac{1}{2}m{\left( {{v_{\min }}} \right)^2} + \left[ { - \dfrac{{16GMm}}{{2a}} - \dfrac{{GMm}}{{\left( {10a - 2a} \right)}}} \right] = 0 + \left( { - \dfrac{{16GMm}}{{{r_2}}} - \dfrac{{GMm}}{{{r_2}}}} \right) \\\$$

(Here, ${v_{\min }}$ is the minimum initial speed of the body to reach the surface of the smaller star. Also, there is no kinetic energy at point R.

$$\Rightarrow \dfrac{1}{2}m{\left( {{v_{\min }}} \right)^2} = \dfrac{{16GMm}}{{2a}} + \dfrac{{GMm}}{{8a}} - \dfrac{{16GMm}}{{8a}} - \dfrac{{GMm}}{{2a}} \\\ \Rightarrow \dfrac{1}{2}m{\left( {{v_{\min }}} \right)^2} = \dfrac{{GMm}}{{2a}}\left( {16 + \dfrac{1}{4} - 4 - 1} \right) \\\ \Rightarrow \dfrac{1}{2}m{\left( {{v_{\min }}} \right)^2} = \dfrac{{45GMm}}{{8a}} \\\ \Rightarrow {v_{\min }} = \sqrt {\dfrac{{45GM}}{{4a}}} \\\ \therefore {v_{\min }} = \dfrac{{3\sqrt 5 }}{2}\sqrt {\dfrac{{GM}}{a}} \\\$$

Thus, minimum initial speed of the body to reach the surface of the smaller star is $\dfrac{{3\sqrt 5 }}{2}\sqrt {\dfrac{{GM}}{a}}$.

Note: Here, we have determined the minimum initial speed of the body to reach the surface of the smaller star when it is minimum initial speed of the body to reach the surface of the smaller star. From the obtained answer, it is clearly seen that this minimum velocity is dependent on the Gravitational constant $G$, mass of the smaller star $M$ and radius of the smaller star $a$. Also it is independent of the mass of the body $m$.