Question
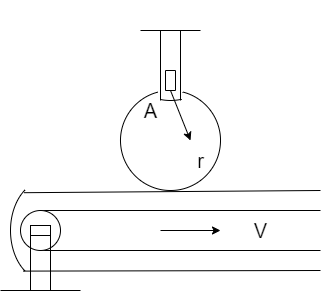
Question: Disk A has a mass of \(4kg\) and a radius \(r = 75mm\), it is at rest, when it is placed in contact ...
Disk A has a mass of 4kg and a radius r=75mm, it is at rest, when it is placed in contact with the belt which moves at a constant speed v=18m/s. Knowing that μk=0.25 between the disk and the belt, determine the number of revolutions executed by the disk before it reaches a constant angular velocity. (Assume that the normal reaction by the belt on the disc is equal to weight of the disc).
Solution
Recall that torque is defined as the amount of force required to cause the rotation of an object. Also when the belt and disc are in contact with each other then, the disc experiences a force of kinetic friction in a direction opposite to the direction of its motion. This is known as kinetic friction.
Complete step by step solution:
Step I:
Given that the
Mass of the disc is M=4kg
Radius of disc R=75×10−3m
Speed of belt, v=18m/s
Coefficient of kinetic friction μk=0.25
Step II:
Since kinetic friction occurs, so the force between belt and disc is equal to the weight. Therefore, the amount of torque due to friction will be
τ=μk×R
Substituting the values in the formula,
⇒ τ=0.25×40×75×10−3
⇒ τ=0.75Nm
Step III:
According to Newton’s second law of motion, the net force acting on an object is directly proportional to the mass and the acceleration of the object. Applying Newton’s second law,
τ=Iα
Where I is the moment of inertia
And αis the angular acceleration of the disc
⇒ 0.75=2MR2×α
⇒ 10075=24×5625×10−6α
⇒ α=4×75×1002×104
⇒ α=4×75×1002×10000
⇒ α=3002×100
⇒ α=66.66%
Step IV:
Also the angular velocity of an object means how fast an object rotates with respect to some reference point. It depends on how fast the object changes its position with time. Therefore, angular velocity is given as
⇒ ω=rV
⇒ ω=7518×10−3
⇒ ω=758000=240
Step V:
⇒ ω2=2αθ
⇒ θ=2αω2
⇒ θ=2×66.66(240)2
⇒ θ=137.52
The number of revolutions are 137.52.
Note: It is important to remember that the term kinetic friction is also known as sliding friction. This type of friction is very important for moving objects. Also the magnitude of the frictional force will depend on the coefficient of kinetic friction of the two bodies in contact. The coefficient of kinetic friction is unitless and represented by the symbol ‘mu’ with subscript ‘k’, μk.
