Solveeit Logo
Login

Question

Question: Discuss motion of a car along a banked road with figure and show that \({{R}_{g}}{{(\dfrac{{{\mu }_{...

Discuss motion of a car along a banked road with figure and show that Rg(μs+tan⁡θ1−μtan⁡θ)1/2{{R}_{g}}{{(\dfrac{{{\mu }_{s}}+\tan \theta }{1-\mu \tan \theta })}^{1/2}}

Explanation

Solution

Banking of roads is the state in which the edges of the curved roads are raised above the inner edge to ensure centripetal force for automobiles, so that the safety is ensured when they take a turn. The angle at which the inclination is maintained is called the bank angle.

Complete step by step answer:
When roads are banked and when a car moves along the road, the centripetal force is provided by the horizontal component of the normal reaction. In normal cases, that is when a car travels through an unbanked, horizontally curved road, the frictional force between the wheels and the surface of the road acts as the centripetal force. But sometimes it is insufficient when the nature of the road changes, especially when it is oily or wet. The roads can’t be made rough either, as it causes wear and tear to the tyres.
The major advantage of banking is that it avoids skidding of the vehicle.

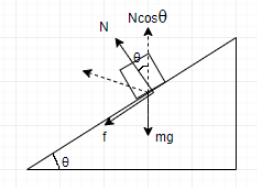
Here, N is the normal force and f is the frictional force.
From the diagram,
Ncos⁡θ=mg+fsin⁡θN\cos \theta =mg+f\sin \theta - - - - - - - - - - - - - - - - - - - - -(1)
And, fcos⁡θ+Nsin⁡θ=mv2rf\cos \theta +N\sin \theta =\dfrac{m{{v}^{2}}}{r} - - - - - - - - - - - - - -(2)
Also, f=μNf=\mu N - - - - - - - - - - - - - - - - - - - - - - - - -(3)
Ncos⁡θ=μNsin⁡θ+mg ⇒N(cos⁡θ−μsin⁡θ)=mg  N\cos \theta =\mu N\sin \theta +mg \\\ \Rightarrow N(\cos \theta -\mu \sin \theta )=mg \\\
⇒N=mgcos⁡θ−μsin⁡θ\Rightarrow N=\dfrac{mg}{\cos \theta -\mu \sin \theta } - - - - - - - - - - - - - - - (4)
Substitute (3) and (4) in (2)

μmgcos⁡θcos⁡θ−μsin⁡θ+mgsin⁡θcos⁡θ−μsin⁡θ=mv2r ⇒μmgrcos⁡θ+mgrsin⁡θ=mv2cos⁡θ−μmv2sin⁡θ ⇒μmgr+mgrtan⁡θ=mv2−μmv2tan⁡θ ⇒mgr(μ+tan⁡θ)=mv2(1−μtan⁡θ) ⇒v2=rg(μ+tan⁡θ)(1−μtan⁡θ) ∴v=rg(μ+tan⁡θ)(1−μtan⁡θ) \dfrac{\mu mg\cos \theta }{\cos \theta -\mu \sin \theta }+\dfrac{mg\sin \theta }{\cos \theta -\mu \sin \theta }=\dfrac{m{{v}^{2}}}{r} \\\ \Rightarrow \mu mgr\cos \theta +mgr\sin \theta =m{{v}^{2}}\cos \theta -\mu m{{v}^{2}}\sin \theta \\\ \Rightarrow \mu mgr+mgr\tan \theta =m{{v}^{2}}-\mu m{{v}^{2}}\tan \theta \\\ \Rightarrow mgr(\mu +\tan \theta )=m{{v}^{2}}(1-\mu \tan \theta ) \\\ \Rightarrow {{v}^{2}}=\dfrac{rg(\mu +\tan \theta )}{(1-\mu \tan \theta )} \\\ \therefore v=\sqrt{\dfrac{rg(\mu +\tan \theta )}{(1-\mu \tan \theta )}} \\\

Hence, it is proved.

Note: In questions like this, it is always essential to approach the given conditions using a free body diagram as it makes the process easier. This diagram depicts the relative magnitude and direction of all forces acting on the body.