Question

Differentiate $y = \log \left( x + \sqrt{x^2 + a^2} \right)$ w.r.t. $x$.

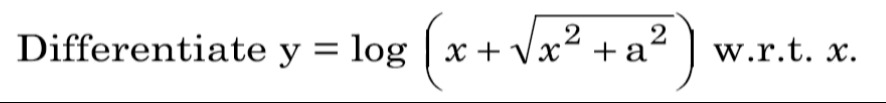
Answer 1

$\frac{1}{\sqrt{x^2 + a^2}}$

Answer 2

Let $y = \log \left( x + \sqrt{x^2 + a^2} \right)$. Assuming $\log$ is the natural logarithm $\ln$.

Using the chain rule, $\frac{dy}{dx} = \frac{1}{u} \cdot \frac{du}{dx}$, where $u = x + \sqrt{x^2 + a^2}$.

The derivative of $u$ is $\frac{du}{dx} = \frac{d}{dx}(x) + \frac{d}{dx}(\sqrt{x^2 + a^2})$. $\frac{d}{dx}(x) = 1$. For $\frac{d}{dx}(\sqrt{x^2 + a^2})$, use the chain rule again: $\frac{1}{2\sqrt{x^2 + a^2}} \cdot \frac{d}{dx}(x^2 + a^2) = \frac{1}{2\sqrt{x^2 + a^2}} \cdot (2x) = \frac{x}{\sqrt{x^2 + a^2}}$.

So, $\frac{du}{dx} = 1 + \frac{x}{\sqrt{x^2 + a^2}} = \frac{\sqrt{x^2 + a^2} + x}{\sqrt{x^2 + a^2}}$.

Substituting back: $\frac{dy}{dx} = \frac{1}{x + \sqrt{x^2 + a^2}} \cdot \left( \frac{x + \sqrt{x^2 + a^2}}{\sqrt{x^2 + a^2}} \right) = \frac{1}{\sqrt{x^2 + a^2}}$.