Solveeit Logo
Login

Question

Question: Differentiate $x^{\sin x} + (\sin x)^x$ w.r.t. $x$....

Differentiate xsin⁡x+(sin⁡x)xx^{\sin x} + (\sin x)^x w.r.t. xx.

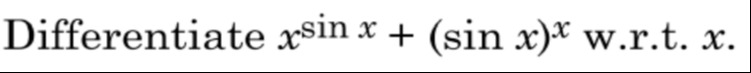
Answer

xsin⁡x(cos⁡xln⁡x+sin⁡xx)+(sin⁡x)x(ln⁡(sin⁡x)+xcot⁡x)x^{\sin x} \left( \cos x \ln x + \frac{\sin x}{x} \right) + (\sin x)^x \left( \ln(\sin x) + x \cot x \right)

Explanation

Solution

Let y=xsin⁡x+(sin⁡x)xy = x^{\sin x} + (\sin x)^x. Let y1=xsin⁡xy_1 = x^{\sin x}. Then ln⁡y1=sin⁡xln⁡x\ln y_1 = \sin x \ln x. Differentiating, 1y1dy1dx=cos⁡xln⁡x+sin⁡xx\frac{1}{y_1} \frac{dy_1}{dx} = \cos x \ln x + \frac{\sin x}{x}. So, dy1dx=xsin⁡x(cos⁡xln⁡x+sin⁡xx)\frac{dy_1}{dx} = x^{\sin x} \left( \cos x \ln x + \frac{\sin x}{x} \right). Let y2=(sin⁡x)xy_2 = (\sin x)^x. Then ln⁡y2=xln⁡(sin⁡x)\ln y_2 = x \ln(\sin x). Differentiating, 1y2dy2dx=ln⁡(sin⁡x)+xcos⁡xsin⁡x\frac{1}{y_2} \frac{dy_2}{dx} = \ln(\sin x) + x \frac{\cos x}{\sin x}. So, dy2dx=(sin⁡x)x(ln⁡(sin⁡x)+xcot⁡x)\frac{dy_2}{dx} = (\sin x)^x \left( \ln(\sin x) + x \cot x \right). Thus, dydx=dy1dx+dy2dx=xsin⁡x(cos⁡xln⁡x+sin⁡xx)+(sin⁡x)x(ln⁡(sin⁡x)+xcot⁡x)\frac{dy}{dx} = \frac{dy_1}{dx} + \frac{dy_2}{dx} = x^{\sin x} \left( \cos x \ln x + \frac{\sin x}{x} \right) + (\sin x)^x \left( \ln(\sin x) + x \cot x \right).