Question

Diameter of the plano-convex lens is 6 cm and thickness at the centre is 3 mm. If speed of light in material of lens is 2×10$^{8}$ m/s, the focal length of the lens is:
A. 20 cm
B. 30 cm
C. 10 cm
D. 15 cm

Answer 1

First find the refractive index in the given medium, now try to figure out how the lens looks like and draw an imaginary lens without the plane surface, by doing this we can find the radius of the lens, now apply this radius and refractive index that we have got to the formula for focal length of a lens in a given medium.

Complete step by step answer:
We know that the refractive index of the lens is:
$\mu =\dfrac{c}{v}$ , here c is the speed of light, and v is the speed of light in the given medium.
$\mu =\dfrac{3\times {{10}^{8}}}{2\times {{10}^{8}}}$,
$\mu =1.5$, this is the refractive index of the lens.
Now, we know that the lens given is a plano-convex lens, which means that the lens is convex on one side and plane on another,

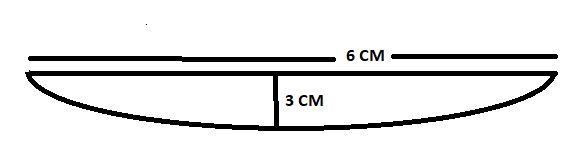
This is the plano convex lens, with 6 cm as the diameter and 3 cm as the thickness at the center.
Now on extending the surface of the lens, we get

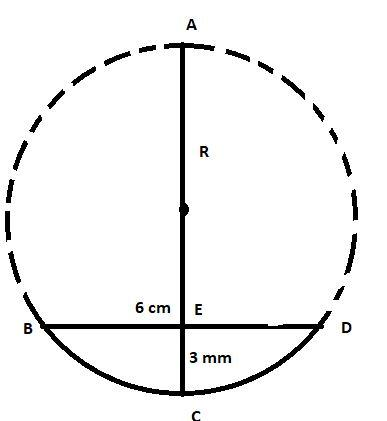
Now we know that in a circle,
BE $\times$ ED = AE $\times$ CE
9=(R + R -0.3) $\times$0.3,
30 = 2R – 0.3,
R=3.03/15,
Therefore we find R to be nearly 15 cm.
Now we know that focal length is:
$\dfrac{1}{f}=(\mu -1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ ,${{R}_{2}}$is equals to infinity.
$\dfrac{1}{f}=(1.5-1)\left( \dfrac{1}{15}-\dfrac{1}{\infty } \right)$,
$\dfrac{1}{f}=(\dfrac{1}{2})\left( \dfrac{1}{15}-0 \right)$,
Therefore focal length of the lens is,
F=30cm
Therefore option B is the correct option.

Note: ${{R}_{2}}$ is equal to infinity, the lens given is a plano convex lens that is a lens with convex on one side and plane on another. Students must remember that anything divided by infinity is equals to zero.