Question
Question: Diagonals LS and BN of rectangle BSNL intersect each other at point K. If \[{\text{KL}} = 7{\text{ c...
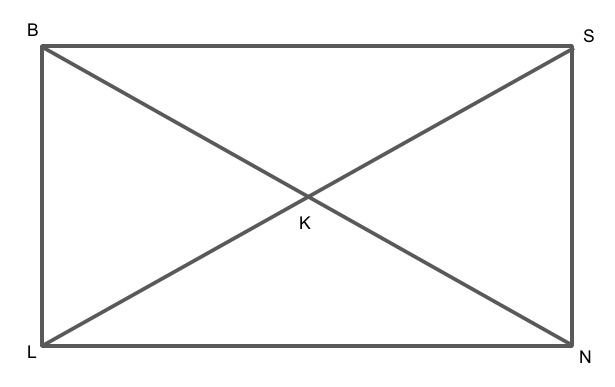
Diagonals LS and BN of rectangle BSNL intersect each other at point K. If KL=7 cm, find LS and BN. (see figure)
Solution
First we will use that in parallelogram BSNL, the sides BS and LN are equal and BS||LN by our given diagram. In triangles ΔLKN and ΔSBK, if BS||LN and BN is the transversal ∠LNK and ∠SBK being the alternate angles are equal and SL is the transversal ∠KLN and ∠KSB being the alternate angles are equal. As the line segment BS is equal to LN, we have BS=LN. Then use ASA rule, to prove the angles to be congruent. Then use the corresponding parts of congruent triangles to prove the line segments KL and SK are equal.
Then use LS=2KL to find the value of LS and then rectangle property to find the value of BN.
Complete step by step answer:
We are given that the diagonals LS and BN of rectangle BSNL intersect each other at point K.

We know that in parallelogram BSNL, the sides BS and LN are equal and BS||LN by our above construction.
Consider triangles ΔLKN and ΔSBK,
We know that if BS||LN and BN is the transversal ∠LNK and ∠SBK being the alternate angles, we have
⇒∠LNK=∠SBK
We also know that if BS||LN and SL is the transversal ∠KLN and ∠KSB being the alternate angles, we have
⇒∠KLN=∠KSB
As the line segment BS is equal to LN, we have BS=LN.
We know that in AAS rule, when two angles and a side of two triangles are same, then the both triangles are congruent with each other.
Using the above AAS rule, we get
∴ΔLKN≅ΔSKB
Being the corresponding parts of congruent triangles ΔLKN and ΔSKB, the line segments KL and SK are equal.
We are given that KL is 7 cm.
This implies that LS=2KL.
Substituting the given value of KL in the above equation, we get
We know that in a rectangle both the diagonals are equal, so BN is equal to LS.
⇒BN=14 cm
Note: In solving these types of questions, you need to know that the properties of rectangles and their diagonals. Then we will use the properties accordingly. This is a simple problem, one should only need to know the definitions. It is clear from the diagram that it is a rectangle as nowhere it is given it to be a square, so remember that as well.
