Solveeit Logo
Login

Question

Question: \( \dfrac{F-32}{180}=\dfrac{40-0}{100}={{104}^{\circ }}F \) Illustration \( 2 \) : Cabronhait sca...

F−32180=40−0100=104∘F\dfrac{F-32}{180}=\dfrac{40-0}{100}={{104}^{\circ }}F
Illustration 22 : Cabronhait scale reading equal to twice of Celsius.

Explanation

Solution

Hint : In order to solve this question, we are going to simplify the relation given first which gives us the value in Fahrenheit and then also calculate its Celsius equivalent and then we find the temperature in Fahrenheit for which its Celsius equivalent is exactly equal to half of its value in Fahrenheit.
The temperature in Fahrenheit can be converted to that in degrees Celsius by using the formula
(∘F−32)×59=∘C\left( ^{\circ }F-32 \right)\times \dfrac{5}{9}{{=}^{\circ }}C
And temperature in degree Celsius can be converted to that in Fahrenheit by using the formula
(∘C×95)+32=∘F\left( ^{\circ }C\times \dfrac{9}{5} \right)+32{{=}^{\circ }}F .

Complete Step By Step Answer:
As the equation is given, if we simplify the equation, we get
F−32180=40−0100 F−32180=40100 F−32180=25 5F−160=360 5F=520 F=5205 ⇒F=104 \begin{aligned} & \dfrac{F-32}{180}=\dfrac{40-0}{100} \\\ & \dfrac{F-32}{180}=\dfrac{40}{100} \\\ & \dfrac{F-32}{180}=\dfrac{2}{5} \\\ & 5F-160=360 \\\ & 5F=520 \\\ & F=\dfrac{520}{5} \\\ & \Rightarrow F=104 \\\ \end{aligned}
So, we get the value of Fahrenheit from this equation equal to the temperature 104∘F{{104}^{\circ }}F
Its Celsius equivalent is
(104∘F−32)×59 ⇒72×59∘C=40∘C \begin{aligned} & \left( {{104}^{\circ }}F-32 \right)\times \dfrac{5}{9} \\\ & \Rightarrow 72\times {{\dfrac{5}{9}}^{\circ }}C={{40}^{\circ }}C \\\ \end{aligned}
The temperature in Fahrenheit is equal to the twice of the reading in degree Celsius for 320∘F{{320}^{\circ }}F , which is equal to 160∘C{{160}^{\circ }}C ,
This can be proved by using the formula for conversion of Fahrenheit to Celsius which is further given by
(∘F−32)×59=∘C\left( ^{\circ }F-32 \right)\times \dfrac{5}{9}{{=}^{\circ }}C
Now putting the values in the relation, we get
Hence, the Fahrenheit equivalent of 160∘C{{160}^{\circ }}C is 320∘F{{320}^{\circ }}F , i.e. it is equal to twice of the value.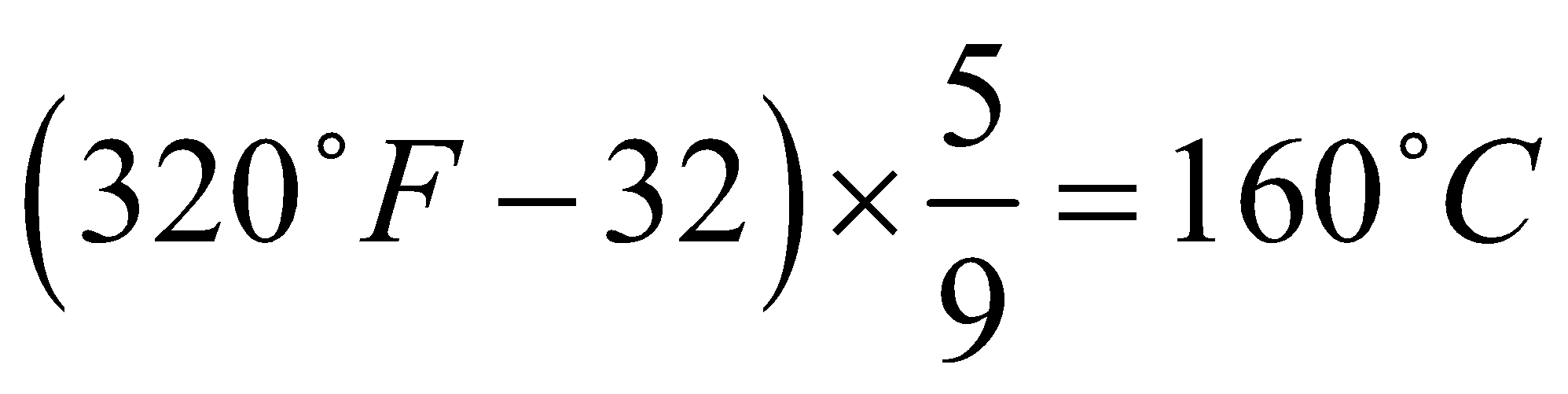

Note :
The step where we are simplifying the given relation to prove that the value is exactly the same as given in the question is very important and hence to be solved very carefully also, just stating which temperature is twice of its equivalent in Celsius is not enough, we really need to prove it using formula also.