Question

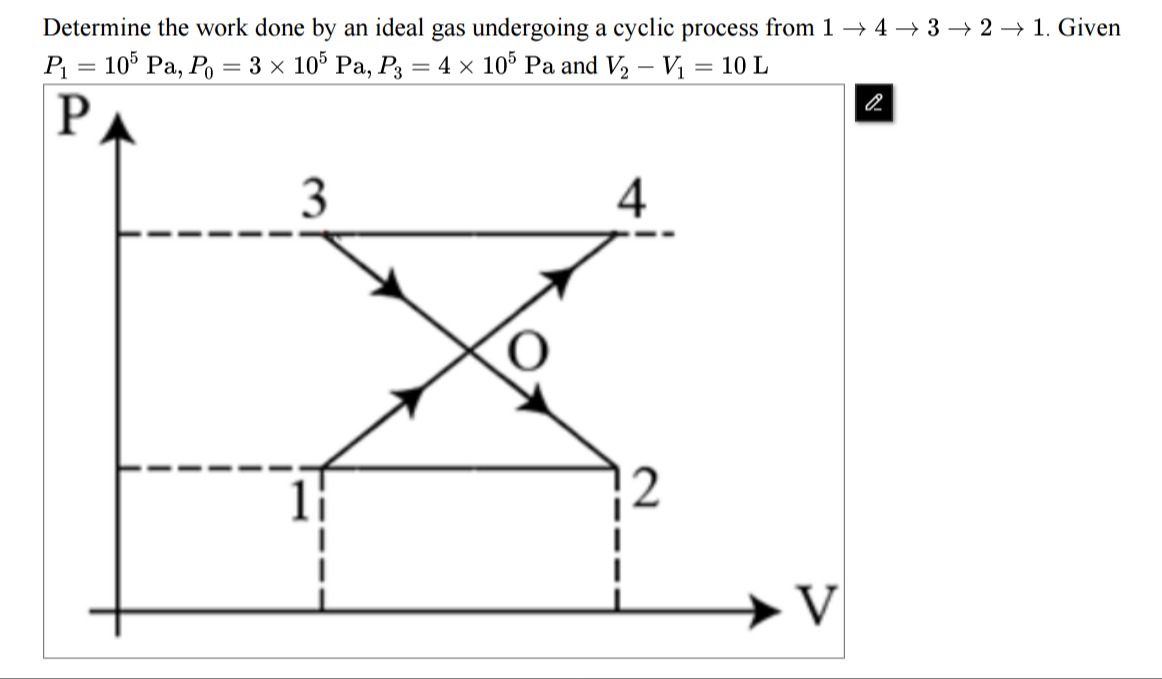
Determine the work done by an ideal gas undergoing a cyclic process from 1→4→3→2→ 1. Given $P_1 = 10^5$ Pa, $P_0 = 3 \times 10^5$ Pa, $P_3 = 4 \times 10^5$ Pa and $V_2 - V_1 = 10$ L

Answer 1

750 J

Answer 2

We will show that the net work done in the cycle is equal to the area enclosed in the P–V diagram. In our problem the cycle is given by the vertices (with pressures and volumes as follows):

• Point 1: (V₁, P₁ = 10⁵ Pa)
• Point 2: (V₂, P₁ = 10⁵ Pa) with V₂ – V₁ = ΔV = 10 L = 0.01 m³
• Point 3: (V₃, P₃ = 4×10⁵ Pa)
• Point 4: (V₄, P₃ = 4×10⁵ Pa)

The only “extra” given is that the two straight “diagonal” lines (the segments 1→4 and 2→3) meet at a point O which (by the diagram) has pressure P₀ = 3×10⁵ Pa. (That fact is used to “fix” the shape.) One finds that a consistent set of coordinates is obtained by taking

• Point 1: (V₁, 10⁵)
• Point 2: (V₁ + 0.01, 10⁵)
• Point 3: (V₁ + 0.005, 4×10⁵)
• Point 4: (V₁ + 0.01, 4×10⁵)

It is important to note that the cycle is not “simple” but is actually a “bow–tie” (self–intersecting) quadrilateral. To compute the net work done (the area enclosed by the cycle) one may “break up” the path into four pieces and add the work (with appropriate signs) along each leg. Taking work done by the gas as

$W = \int P dV$

we have:

1. Segment 1→4 (straight–line from (V₁,10⁵) to (V₁ + 0.01,4×10⁵))
   Since the process is linear, the work is the area under the curve:
   $W₁ = (½)[P₁ + (4×10⁵)] (ΔV) = (½)[10⁵ + 4×10⁵] (0.01) = (½)[5×10⁵]×0.01 = 2500 J$.
2. Segment 4→3 (horizontal at 4×10⁵, going from V = V₁+0.01 to V = V₁+0.005, so ΔV = –0.005 m³)
   $W₂ = 4×10⁵ × (–0.005) = –2000 J$.
3. Segment 3→2 (linear from (V₁+0.005,4×10⁵) to (V₁+0.01,10⁵); ΔV = 0.005 m³)
   The work is:
   $W₃ = (½)[4×10⁵ + 10⁵] (0.005) = (½)[5×10⁵]×0.005 = 1250 J$.
4. Segment 2→1 (horizontal at 10⁵, from V = V₁+0.01 back to V = V₁; ΔV = –0.01 m³)
   $W₄ = 10⁵ × (–0.01) = –1000 J$.

Now, the net work done in one complete cycle is the sum

$W = W₁ + W₂ + W₃ + W₄ = 2500 – 2000 + 1250 – 1000 = 750 J$.

Thus the work done by the gas in completing the cycle is 750 J.

Minimal Explanation

1. Assign coordinates:
   Point 1 = (V₁,10⁵), Point 2 = (V₁+0.01,10⁵), Point 4 = (V₁+0.01,4×10⁵), Point 3 = (V₁+0.005,4×10⁵) (using the fact that the diagonal lines intersect at P = 3×10⁵).
2. Compute work on each segment assuming linear variation (work for linear path = ½(P_initial+P_final)ΔV when ΔV > 0; use sign of ΔV when volume decreases).
3. Sum: 2500 J – 2000 J + 1250 J – 1000 J = 750 J.