Question

Determine the wavelength of the wave caused by the rope whose one end is attached to a tree and other end is swung by a person as shown below:

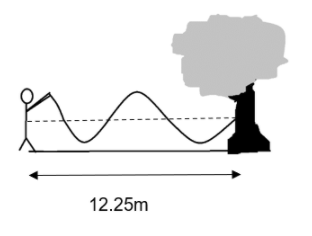
A) 8 m
B) 7 m
C) 6 m
D) 5 m

Answer 1

The wavelength of the rope can be determined by using the total length of the column from the man to the tree. The experiment looks similar to a string attached at one end. We need to see the number of waves involved and thus, calculate the wavelength.

Complete answer:
Let us consider the harmonics involved in a vibration of longitudinal waves. We know that they have strict conditions when the ends are open or closed. In the case of the transverse waves, the node and antinodes are formed with respect to the source.
Let us consider our figure. In order to find the wavelength of the rope wave, we need to find the number of wavelengths that the rope creates with the tree.
On close observation, we can conclude that there is only one complete wave in the figure.

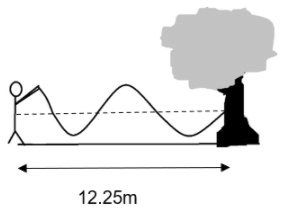
Other than the full wave, there is three-quarters of another wave. So, we can say that the total waves in the rope is $(1+\dfrac{3}{4})\lambda$. This can be further equated to the total length of the column between the man and the tree.
i.e.,
$L=(1+\dfrac{3}{4})\lambda$
From this equation we can get the wavelength of the rope wave as –

& L=(1+\dfrac{3}{4})\lambda \\\ & Given\text{ L =12}\text{.25m} \\\ & \Rightarrow \lambda \text{=}\dfrac{4L}{7} \\\ & \Rightarrow \lambda \text{=}\dfrac{4\times 12.25}{7} \\\ & \Rightarrow \lambda \text{=}7m \\\ \end{aligned}$$ Therefore. The wavelength of the rope wave in the given figure has a wavelength of 7m. **The correct answer is option B.** **Additional Information:** The wavelength depends on the number of harmonics between the two ends of the rope. **Note:** For the same rope, we can have a longer wavelength if the number of oscillations is further reduced. The wavelength will be equal to the length if the number of waves is 1. The frequency increases as the number of waves increases and that decreases the wavelength.