Question

Determine the total pressure on a circular plate of diameter 1.5 m which is placed vertically in water in such a way that the centre of plate is 2 m below the free surface of water. Find the position of centre of pressure also.

Answer 1

We need to find the total pressure and the position of centre of pressure of the given circular plate. To find the pressure we know the expression for pressure. By substituting the known values in the equation we get the pressure on the plate. And to find the position of centre of pressure also we know the equation. We also know the equation to find the moment of inertia about the horizontal axis through the centre of gravity. By finding this moment of inertia and substituting, we get the position of centre of pressure.

Formula used:
Pressure, $F=\rho ghA$
Position of centre of pressure, $h*=\dfrac{{{I}_{G}}}{Ah}+h$

Complete step by step answer:
In the question we are given a circular plate of diameter 1.5 m
It is said that this circular plate is immersed vertically in water in such a way that the centre of the plate is 2 m below the surface of water.

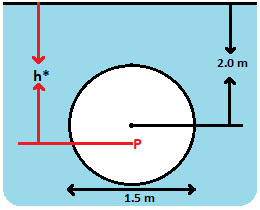
The given situation is depicted in the above figure.
The point ‘P’ in the figure is the centre of pressure and ‘h*’ determines the position of centre of pressure.
First let us find the total pressure experienced by the circular plate.
The total pressure is given by the equation,
$F=\rho ghA$, where ‘’F’ is the force, ‘$\rho$’ is density, ‘g’ is acceleration due to gravity, ‘h’ is the height and ‘A’ is area.
In the given case, we know that,
‘$\rho$’ is the density of water and we know that density of water is $1000kg/{{m}^{3}}$
We can take value of acceleration due to gravity as $g=10m/s$
‘h’ is the height from the free surface to the centre of the plate which is given as 2.0 m
Area ‘A’ is the area of the plate given as $A=\dfrac{\pi {{d}^{2}}}{4}$, were ‘d’ is the diameter of the plate which is = 1.5 m
Therefore by substituting all this known values in the equation, we get
$\Rightarrow F=\left( 1000\times 10\times 2 \right)\dfrac{\pi \times \left( {{1.5}^{2}} \right)}{4}$

& \Rightarrow F=20000\times \dfrac{3.14\times {{1.5}^{2}}}{4} \\\ & \Rightarrow F=20000\times 1.767 \\\ \end{aligned}$$ $$\Rightarrow F=3.5342\times {{10}^{4}}N$$ Hence we got the total pressure on the circular plate as $$3.5342\times {{10}^{4}}N$$ Now we need to find the position of centre of pressure. We know that the equation for centre of pressure is given by the equation, $$h*=\dfrac{{{I}_{G}}}{Ah}+h$$, were ‘${{I}_{G}}$’ is the moment of inertia of the plate about its horizontal axis through its centre of gravity and ‘h’ is the distance from the free surface to the centre of the plate which is given as 2.0 m We know that ‘${{I}_{G}}$’ is given as, ${{I}_{G}}=\dfrac{\pi {{d}^{4}}}{64}$ And from previous calculations we know, area $A=1.767{{m}^{2}}$ By substituting for diameter in the above equation, we get $\Rightarrow {{I}_{G}}=\dfrac{3.14\times {{1.5}^{4}}}{64}$ $\Rightarrow {{I}_{G}}=0.2485{{m}^{4}}$ Now we can calculate the value of ‘h*’ $$\Rightarrow h*=\left( \dfrac{0.2485}{\left( 1.767\times 2 \right)} \right)+2$$ $$\Rightarrow h*=0.0703+2$$ $$\Rightarrow h*=2.0703m$$ Thus we got the position of centre of pressure of the plate as, 2.0703 m. **Note:** When we calculate the total pressure on the circular disc, we know that the total pressure experienced by the plate will be exerted at the centre of the circular plate. Since we are given the distance from the free surface to the centre of the plate, we use that as the height. Hence the total pressure experienced by the plate is the total pressure experienced at the centre of the plate which is the total force experienced at the centre of the plate.