Question

Determine the time in which the smaller block reaches the other end of the bigger block in the figure:

$(A)4{\text{ }}s$
$(B)8{\text{ }}s$
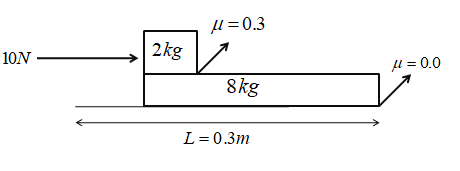
$(C)2.19{\text{ }}s$
$(D)13{\text{ }}s$

Answer 1

To solve this question one must be aware of the relation between force and acceleration. In addition to this, one must also know the equation of motion. First, the coefficient of friction acting between the blocks must be calculated using the coefficient value. Then one must calculate the individual acceleration of both the blocks. After acceleration of the block with a mass with respect to block A should be calculated. Finally, substitute this value of acceleration in the equation of motion to obtain the value of time.
Formula used:
$F = ma$ ; $S = ut + \dfrac{1}{2}a{t^2}$
Where
$F$ stands for the force, $m$ is mass,
$a =$ acceleration, $S =$ distance, $u =$ initial velocity, $t =$ time

Complete step by step answer:
Let the block with mass ${\text{8 kg}}$ be denoted as block A and the block with mass ${\text{2 kg}}$ be denoted as block B.

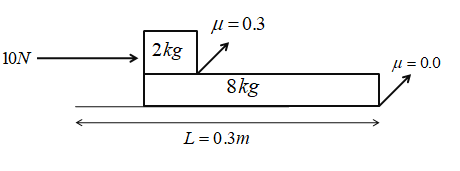
Let’s determine the coefficient of friction
$\text{Coefficient of friction} = \mu mg$
Where, ${\mu = 0}{\text{.3, m = 2 Kg}}$
And, acceleration due to the gravity, ${\text{g = 10N}}$
Therefore by substituting the given values in the expression we obtain;
${\text{coefficient of friction = 0}}{\text{.3}} \times {\text{2}} \times {\text{10}}$
After multiplying we obtain the value of ${\text{coefficient of friction = 6 N}}$
The acceleration acting on block A, ${{\text{a}}_{\text{A}}}{\text{ = }}\dfrac{{\text{F}}}{{\text{M}}}$
By substituting the value of ${\text{coefficient of friction = 6 N and mass M = 2 Kg}}$
We get, ${{\text{a}}_{\text{A}}}{\text{ = }}\dfrac{6}{8} = {\text{0}}{\text{.75m}}{{\text{s}}^{{\text{ - 2}}}}$
The net force acting on the second block that is block B will be the total force, ${\text{10 N}}$ subtracted with the coefficient of friction.
Therefore we get, ${{\text{F}}_{{\text{net}}}}{\text{ = 10 - 6 = 4N}}$
Now, let’s calculate the acceleration on block B, ${a_B} = \dfrac{{{F_{net}}}}{m}$ . Here ${{\text{F}}_{{\text{net}}}}{\text{ = 4 N and m = 2Kg}}$ .
Substitute the values in the expression for acceleration
${{\text{a}}_{\text{B}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{2}}}{\text{ = 2 m}}{{\text{s}}^{ - 2}}$
Now we have to calculate the relative acceleration of block B with respect to A. To do this, subtract the value of the acceleration of block A from block A.
$a = {a_B} - {a_a}$
$a = 2 - 0.75 = 1.25{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$
Now using the equation of motion we can determine the time taken to reach the end of block B.
The equation of motion, $S = ut + \dfrac{1}{2}a{t^2}$
${\text{The total distance to be covered = 3 m}}$
${\text{acceleration}} = 1.25{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$
Initial velocity, $u = 0{\text{ m}}{{\text{s}}^{ - 1}}$
Substitute the given and obtained values in the equation of motion.
$3 = 0 + \dfrac{1}{2} \times 1.25 \times {t^2}$
By rearranging we get, ${t^2} = \dfrac{6}{{1.25}} = 4.18$
Taking the square root we get, $t = \sqrt {4.18} = 2.19{\text{s}}$
Therefore the time taken for the block to reach the end of the block B is $t = 2.19{\text{s}}$

Hence, the right answer is in option (C).

Note:
Friction is a force that opposes the applied force. Friction takes place in the direction opposite to the direction of motion. There are four types of friction static, sliding, rolling, and fluid friction otherwise known as drag. Friction takes place between the contact surfaces of two objects. If the contact surface is rough, that is more irregular, friction will be more. This is because of a property called interlocking.