Question

Determine the tensions ${T_2}$ ​ and ${T_1}$ ​ in the strings as shown in figure.

(A) $22.6N,45.31N$
(B) $39.2N,78.4N$
(C) $39.2N,67.8N$
(D) $39.2N,45.31N$

Answer 1

Hint
We resolve the tension force in string one into horizontal and vertical components. Since the system is at equilibrium or rest, the force acting upwards is equal to the force acting downwards. Also, the force acting towards the left is equal to the force acting towards the right. The force acting downwards is nothing but the weight of the body, this force is equal to the vertical component of the tension force in string one. We find tension force in string one from this. The tension force acting on string two is equal to the horizontal component of the tension force in string one. The free-body diagram in the complete solution can be referred to for a better understanding.

Complete step by step answer
We resolve the tension force into its horizontal and vertical component as follows,
From alternate exterior angles, we know the angle between the force and the horizontal component of the force.

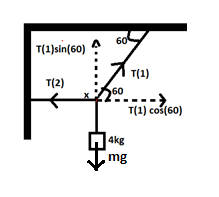
Since the body is in equilibrium
Equating forces in the y-direction
\Rightarrow [{T_1}sin60^\circ = 4 \times 9.8\]
Equating forces in the x-direction
\Rightarrow [{T_1}cos60^\circ = {T_2}\]
Tension force on string one is
$\Rightarrow {T_1} = \dfrac{{4 \times 9.8}}{{\sin 60^\circ }} = \dfrac{{4 \times 9.8 \times 2}}{{\sqrt 3 }}$
$\Rightarrow {T_1} = 45.26N$
Tension on string two is
$\Rightarrow {T_2} = {T_1}cos60^\circ$
$\Rightarrow {T_2} = 45.26 \times \dfrac{1}{2}$
$\Rightarrow {T_2} = 22.63N$
Tension forces on string one and string two are $45.26N,22.63N$ respectively.
Hence option (A) $22.6N,45.31N$ is the correct answer.

Note
We can also solve this problem using Lami's theorem. Lami's theorem states that when three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces. Referring to the above diagram, consider three forces A, B, C acting on a particle or rigid body making angles α, β, and γ with each other. The mathematical statement of Lami’s theorem is $\dfrac{A}{{\sin \propto }} = \dfrac{B}{{\sin \beta }} = \dfrac{C}{{\sin \gamma }}$ .