Question

Determine the rms value of a semi-circular current wave which has a maximum value of a

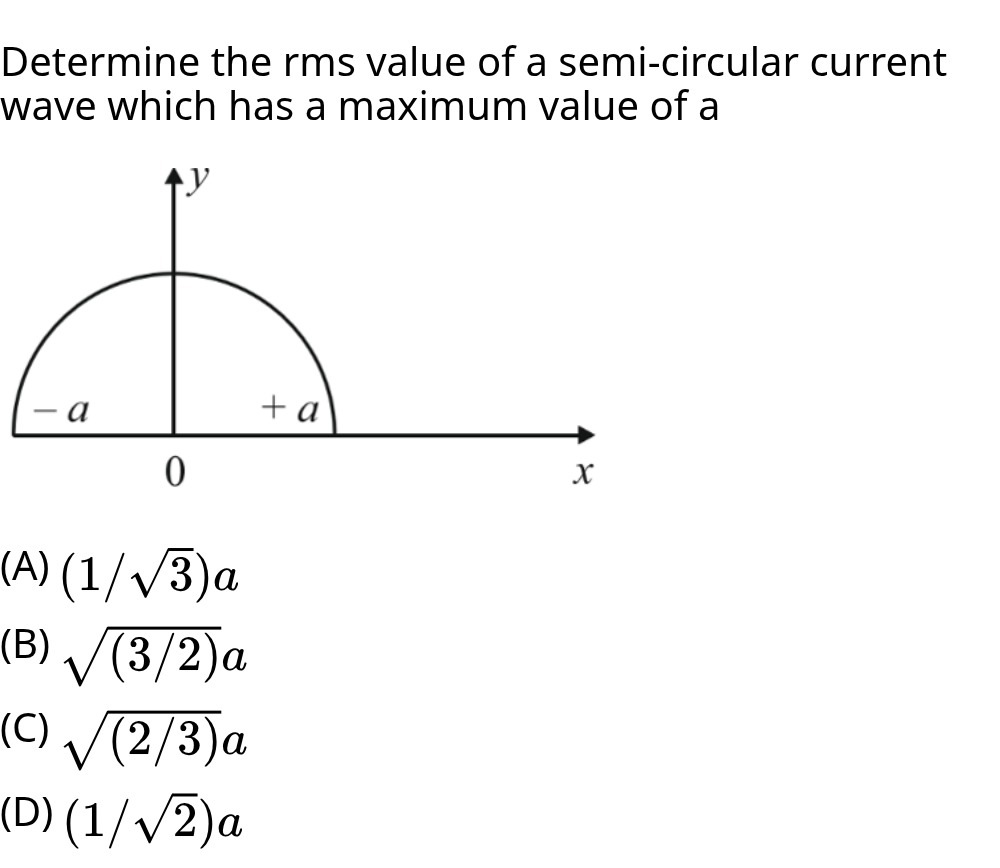
• A. (1/$\sqrt{3}$)a
• B. $\sqrt{(3/2)}$a
• C. $\sqrt{(2/3)}$a
• D. (1/$\sqrt{2}$)a

Answer 1

Answer: (C)

$\sqrt{(2/3)}$a

Answer 2

The root mean square (RMS) value of a current $I(t)$ over a time interval $T$ is given by: $I_{rms} = \sqrt{\frac{1}{T} \int_0^T I(t)^2 dt}$ For a semi-circular current wave with maximum value 'a', the current can be described by $I(t) = \sqrt{a^2 - t^2}$ for $-a \le t \le a$. The duration of this cycle is $T = 2a$.

The RMS value is calculated as: $I_{rms}^2 = \frac{1}{2a} \int_{-a}^{a} (\sqrt{a^2 - t^2})^2 dt$ $I_{rms}^2 = \frac{1}{2a} \int_{-a}^{a} (a^2 - t^2) dt$ Evaluating the integral: $\int_{-a}^{a} (a^2 - t^2) dt = \left[ a^2t - \frac{t^3}{3} \right]_{-a}^{a} = \left( a^3 - \frac{a^3}{3} \right) - \left( -a^3 + \frac{a^3}{3} \right) = \frac{2a^3}{3} - \left( -\frac{2a^3}{3} \right) = \frac{4a^3}{3}$ Substituting back: $I_{rms}^2 = \frac{1}{2a} \cdot \frac{4a^3}{3} = \frac{2a^2}{3}$ Taking the square root: $I_{rms} = \sqrt{\frac{2a^2}{3}} = a \sqrt{\frac{2}{3}}$