Question

Determine the ratio in which line $2x + y - 4 = 0$ divides the line segment joining the points $A\left( {2, - 2} \right)\,\,and\,\,B\left( {3,7} \right)$

Answer 1

Hint : For this we first let the ratio be $k:1$ then using section formula we first find coordinates of the point which is common on a given line segment and on a given line. Then substituting these coordinates in the given equation of a line to find the value of k or required ratio.
Formulas used: Section formula: $x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\,\,y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}}$

Complete step-by-step answer :
Let the ratio be $k:1$ in which given line $2x + y - 4 = 0$ divides the line segment joining the points
$A\left( {2, - 2} \right)\,\,and\,\,B\left( {3,7} \right)$ .

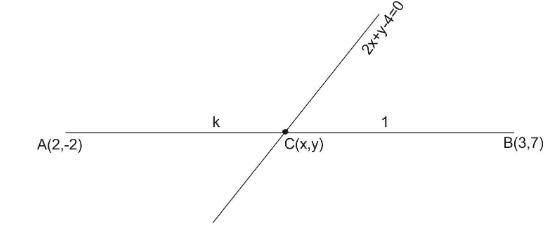
Then, by using the section formula we can find the coordinate of the point which divides the line segment joining the points $A\left( {2, - 2} \right)\,\,and\,\,B\left( {3,7} \right)$ .
Therefore, we have:
$x = \dfrac{{3k + 2}}{{k + 1}},\,\,y = \dfrac{{7k - 2}}{{k + 1}}$
Since, this point is common on line segment joining points $A\left( {2, - 2} \right)\,\,and\,\,B\left( {3,7} \right)$ and line $2x + y - 4 = 0$ .
Therefore, substituting the value of ‘x’ and ‘y’ in the given equation and simplifying to get the value of k.
$2\left( {\dfrac{{3k + 2}}{{k + 1}}} \right) + \left( {\dfrac{{7k - 2}}{{k + 1}}} \right) - 4 = 0 \\\ \Rightarrow \dfrac{{6k + 4}}{{k + 1}} + \dfrac{{7k - 2}}{{k + 1}} - 4 = 0 \\\$
$taking\,\,LCM \\\ \dfrac{{6k + 4 + 7k - 2 - 4\left( {k + 1} \right)}}{{k + 1}} = 0 \\\$

$\Rightarrow \dfrac{{13k + 2 - 4k - 4}}{{k + 1}} = 0 \\\ \Rightarrow \dfrac{{9k - 2}}{{k + 1}} = 0 \\\ \Rightarrow 9k - 2 = 0 \\\ \Rightarrow 9k = 2 \\\ \Rightarrow k = \dfrac{2}{9} \;$
Therefore, from above we can see that the value of k is $\dfrac{2}{9}$ or we can say that ratio is $\dfrac{2}{9}$ .
Hence, we see that line $2x + y - 4 = 0$ divides line segment joining points $A\left( {2, - 2} \right)\,\,and\,\,B\left( {3,7} \right)$ in ratio $\dfrac{2}{9}$ .
So, the correct answer is “ $\dfrac{2}{9}$”.

Note : For this type of problem we can either take the ratio as in terms of $a:b$ and then use the section formula to find coordinates of the points which lie on both line segments joining given points and on a given line. Then substituting the coordinate of this point in the given line to form an equation in terms of a and b then finding the value of $\dfrac{a}{b}$ by dividing the whole equation by b and hence required ratio asked in the given problem.