Question
Question: Determine the pressure difference in tube of non-uniform cross-sectional area as shown in figure \[\...
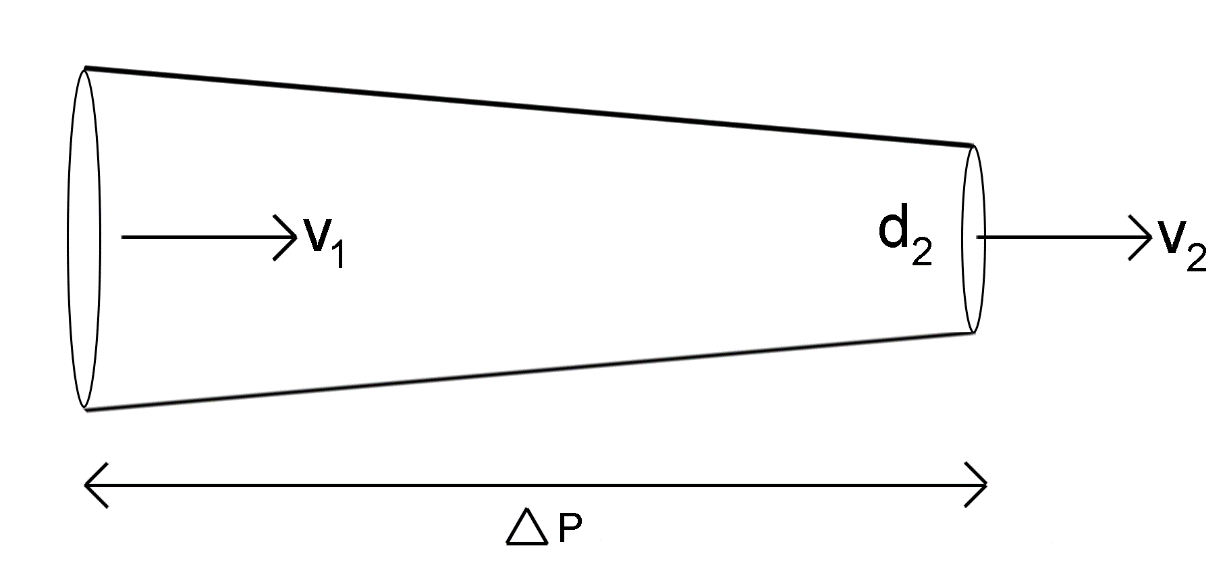
Determine the pressure difference in tube of non-uniform cross-sectional area as shown in figure ΔP=?
d1=5cm,V1=4,d2=2cm,V2=?
(A). 304200Pa
(B). 304500Pa
(C). 302500Pa
(D). 303500Pa
Solution
- Hint: You can start by defining the theory behind the equation A1V1=A2V2 . Use this equation to find d2 . Then use the Bernoulli’s equation i.e. P1+21ρV12+ρgh1=P2+21ρV22+ρgh2 to calculate the pressure difference i.e. P1−P2 .
Complete step-by-step answer:
Before moving on to the mathematical calculations, let’s look at the theory behind the equations which will be used in the equations below.
For an ideal liquid, the product of the area of cross-section and the velocity of the fluid flowing at that point is always constant. This is a very simple concept, the product of the area of cross-section and the velocity of the fluid is equal to the volume of the fluid flowing in that part in 1 second. Now since the volume will always remain constant for any part of the non-uniform cross-sectional area.
Let A1,d1 be the area of cross-section and the radius of the first part. Let A2,d2 be the area of cross-section and the radius of the second part.
We know that,
A1V1=A2V2
\Rightarrow \pi {r_1}^2{V_1} = \pi r_2^2{V_2}$$$$(\because A = \pi {r^2})
⇒(d1)2V1=(d2)2V2
⇒(5)2×4=(2)2×V2
⇒V2=25units
Hence, the velocity of this ideal fluid at the second section is 25units .
We also know by Bernoulli’s equation that
P1+21ρV12+ρgh1=P2+21ρV22+ρgh2
Here,
P1= Pressure at first point,
P2= Pressure at second point,
V1= Velocity of the fluid at first point,
V2= Velocity of the fluid at second point,
ρ=1000kg/m3= Density of water,
h1= Height of the first point,
h2= Height of the second point,
We also know that h1=h2
So, P1+21ρV12=P2+21ρV22
⇒P1−P2=21ρ(V22−V12)
⇒P1−P2=21×1000(625−16)
⇒P1−P2=500(625−16)
P1−P2=304500Pa
P1−P2 is the pressure difference in the tube.
Hence, the pressure difference between the two sections of this non-uniform tube is 304500Pa .
Hence, option B is the correct choice.
Note: All the equations used in the solution above can only be used in this kind of theoretical problem because here it is automatically assumed that the fluid flowing in the given equation is an ideal liquid. But in reality the results from these equations are considerably different as no fluid in reality is an ideal liquid.
