Question

Determine the potential drop between points $A$ and $C$ in the following circuit. Resistance $1\;\Omega$ and $2\Omega$ ( internal resistance of cell)
$(A). \dfrac{4}{5}V$
$(B). 1.75V$
$(C). 2.25{\text{ }}V$
$(D). \dfrac{5}{4}V$

Answer 1

First, the combination of the resistances given here has to be observed and to find the equivalent resistance of the circuit.
Second, the current that flows through the circuit has to be calculated by using the given EMF and equivalent resistance of the circuit.
Finally by using the calculated current find the potential drop of the required terminals.

Formula used:
The equivalent resistance $R = {R_1} + {R_2} + {R_3}$ [ since they are in series connection]
Current flowing through the circuit, $I = \dfrac{{{E_2} - {E_1}}}{R}$
${E_2}$ and ${E_1}$ are two EMFs given in the circuit.
The voltage drop between the two points $A$and $C$, ${V_{AC}} = {E_1} + I{R_1}$

Complete step by step answer:
The circuit given below is showing that two batteries are connected between terminals $C$ and $A$ is $2Volt$, and terminals $A$ and $B$ is $4Volt$. There are two resistances connected along with two batteries and one battery is in series with them.

Let us consider, ${R_1} = 1\Omega ,{R_2} = 2\Omega$ and ${R_3} = 5\Omega$ .
And, ${V_1} = 2V,{V_2} = 4V$
The two EMFs are in opposite directions.

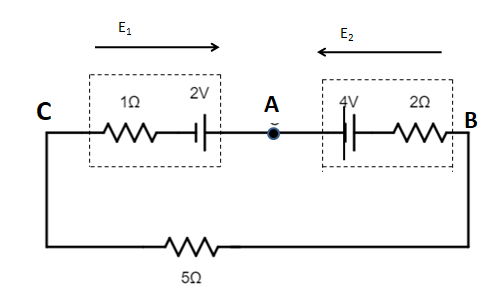
The two EMFs are in opposite directions.
since, ${E_2} > {E_1}$ , the current will flow from point $B$ to $C$.
Hence, The amount of the current flowing through the circuit, $I = \dfrac{{{V_2} - {V_1}}}{R}$
Where, $R$ is the equivalent resistance of the circuit.
$R = {R_1} + {R_2} + {R_3}$
$\Rightarrow R = (1 + 2 + 5) = 8\Omega$
So, $I = \dfrac{{{V_2} - {V_1}}}{R}$
$\Rightarrow I = \dfrac{{4 - 2}}{8}$
$\Rightarrow I = \dfrac{1}{4}$
$\Rightarrow I = \dfrac{{4 - 2}}{8} = 0.25A$
The voltage drop between the two points $A$ and $C$, ${V_{AC}} = {E_1} + I{R_1}$
$\Rightarrow {V_{AC}} = 2 + (0.25 \times 1)$
$\Rightarrow {V_{AC}} = 2.25Volt$
So the potential drop between the two points $A$ and $C$ is $2.25Volt$.

Hence, the correct answer is option (C).

Note:
• If there is no resistance or any source voltage between two points of a circuit, the potential will be the same for two points.
• The EMF can be defined as the difference between the potentials of the two terminals. We can say, the potential of the negative terminal is greater than the positive terminal how much the EMF is.