Question
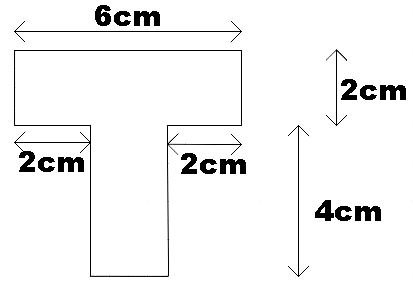
Question: Determine the position of center of mass of the T shaped plate of negligible thickness as shown. !...
Determine the position of center of mass of the T shaped plate of negligible thickness as shown.
Solution
Firstly separate the T-shaped body into two rectangular parts and thus find their respective centre of masses and express their masses in terms of their mass densities. Then, you could place this plate in an x-y coordinate system. Now, you could recall the expression for X and Y coordinates and then substitute accordingly to get the answer.
Formula used: X and Y-coordinates of centre of mass,
X=m1+m2m1x1+m2x2
Y=m1+m2m1y1+m2y2
Complete step by step answer:
In the question we are given a T shaped plate whose thickness is considered negligible being a planar body. Therefore, the whole mass of the plate will be distributed over its area.
The T shaped body could be considered as two triangular parts of mass m1 andm2 put together.

The centre of masses of each part is also marked on the figure. As the mass is equally distributed over the area of the plate, the mass density will be same for both parts and let it be given by m. then,
m1=m×A1=m(6×2)
∴m1=12m …………………………………. (1)
m2=m×A2=m(4×2)
∴m2=8m …………………………………. (2)
The T shaped plate can now be represented on a coordinate axis of x-y plane with O as the origin.
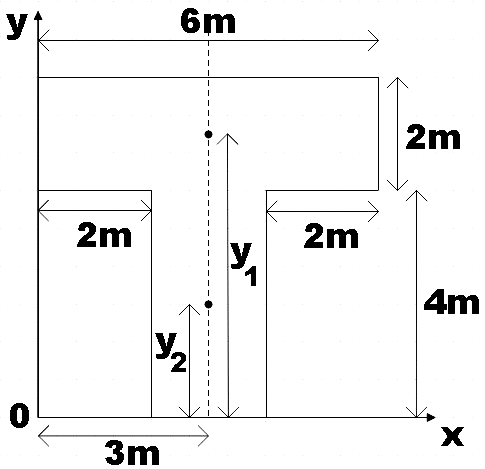
The centre of mass of the whole plate will be on the dotted line connecting the centre of masses of each part (also, by symmetry).
We know that the X and Y coordinates of the centre mass of the system is given respectively as,
X=m1+m2m1x1+m2x2 ……………………………… (3)
Y=m1+m2m1y1+m2y2……………………………….. (4)
Now for the X-coordinate, the centre of masses of each part is equidistant from the origin (3m). So,
X=m1+m23(m1+m2)
Substituting (1) and (2),
X=12+83(12+8)
∴X=3m …………………………………… (5)
Now for the Y-coordinate, centre of masses of parts m1 and m2 are respectively at a distance of y1 and y2 from the origin. So,
Y=m1+m2m1y1+m2y2
From the figure,
y1=5m
y2=2m
Substituting these along with (1) and (2), we get,
Y=12+812×5+8×2
Substituting (1) and (2),
Y=12+860+16
∴Y=3.8m …………………………………… (6)
Therefore, from (5) and (6), we see that the X and Y coordinates of the centre of mass of the T plate is given by,X=3m andY=3.8m.
Hence, the centre of mass of the T-plate is given by,
(X,Y)=(3m,3.8m)
Note: Placing the T-shaped plate in the x-y coordinate system is a must step before making the measurements. The distance of the centre of masses of each part should be measured with respect to the coordinate axes, otherwise you will probably end up in the wrong answer. For example, the distance x2 should be measured from the y-axis as 3m, not the end of the plate as 1m.
