Question

Determine the nature of the lens shown in figure (P) and (Q) given lenses are made from glass and the surrounding medium is air:

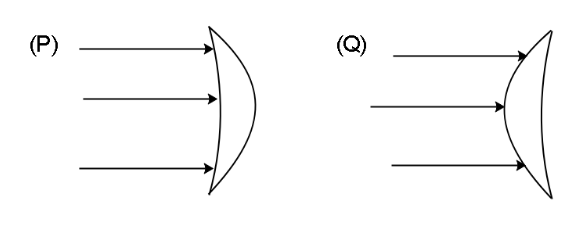
A) P $\to$ converging & Q $\to$ diverging
B) P $\to$ diverging & Q $\to$ converging
C) P & Q both converging
D) P & Q both diverging

Answer 1

Whether a lens is converging or diverging is decided based on whether the lens will converge or diverge parallel rays of light. Converging lenses have a positive focal length and diverging lenses have a negative focal length.

Formula used : In this solution, we will use the following formula
Lens maker formula: $\dfrac{1}{f} = (\mu - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ where $f$ is the focal length of the lens, $\mu$ is the refractive index of the lens placed in the air, and ${R_1},{R_2}$ are the radii of curvature of the two sides of the lens

Complete step by step answer:
In the image given to us, we can observe that both the lenses have two different surfaces with different radius of curvature. Hence to determine the focal length, we will have to use the lens maker formula which is given as:
$\dfrac{1}{f} = (\mu - 1)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Now for the lens in figure (P), we can see that the radius of curvature of both the surfaces is positive and the radius of curvature of the first surface is greater than the radius of curvature of the second surface in magnitude i.e. $\left| {{R_1}} \right| > \left| {{R_2}} \right|$ . Hence in the lens maker formula, we can see that when we invert the relation of ${R_1}$ and ${R_2}$ , we get
$\dfrac{1}{{{R_1}}} < \dfrac{1}{{{R_2}}}$
However, since both ${R_1},{R_2}$ are negative the net term $\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ , will be positive hence the lens in figure (P) will have a positive focal length. So it will be converging in nature.
Similarly, for the lens (Q), both the surfaces have a positive radius of curvature with ${R_1} > {R_2}$ . Hence we can write the relation of the inverse as
$\dfrac{1}{{{R_1}}} < \dfrac{1}{{{R_2}}}$
Hence the term $\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ will be negative so the lens in figure (Q) will have a negative focal length.
So the correct choice is option (B).

Note:
It is by convention that the surfaces that are curved inwards when looking from the left side of the lens have a negative focal length and vice versa. In such cases, it might help to assign arbitrary to numerical values to ${R_1},{R_2}$ determine the value of the term $\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$ as it will decide whether the focal length will be positive or negative.