Question
Question: Determine the force P applied at \[{30^ \circ }\] to the horizontal just necessary to start a roller...
Determine the force P applied at 30∘ to the horizontal just necessary to start a roller having radius 50cm over an obstruction 12cm high. If the roller is of mass 100kg as shown in figure, also find the magnitude of P when it is minimum.
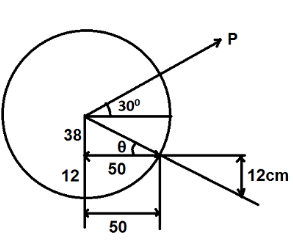
Solution
To solve this problem, we need to use the concept of moment about a point due to forces applied. Here, we will determine the moment about a point where the roller touches the obstruction. We know that to move the roller over the obstruction, the force P should balance the anticlockwise moment due to the weight of the roller about the contact point with the same clockwise moment.
Complete step by step answer:
To solve this question, we will consider the following diagram showing the system of forces required to move the roller over the obstruction.
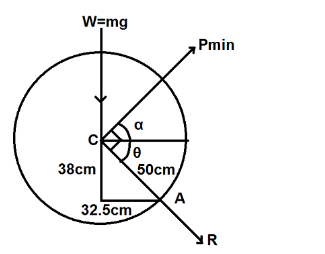
Let A be the contact point of the roller and the obstruction and C be the center of the roller.
From the geometry, we can say that the angle θ can be calculated as:
tanα=32.538=1.169 ⇒θ=tan−11.169=49.46
It is clear from the figure that
α+θ=90 ⇒α=90−49.46=40.54
For the roller to move over the obstruction, the total moment about the point A must be zero.
∑MA=0 ⇒W×32.5−Pmin×50=0 ⇒Pmin=50mg×32.5
We are given that the mass of the roller m=100kg and we will take the gravitational acceleration g=9.81m/s2.
Pmin=50100×9.81×32.5 ∴Pmin=637.65N
Hence, the magnitude of P when it is minimum is 637.65N.
Note: We have considered that the maximum distance between the point A and line of action of P is AC. Therefore, to create a given moment about A, the force P will be minimum when it acts perpendicular to the line AC. That is why we have considered angle α as the direction of the minimum force.
